已知数列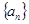 前n项和
前n项和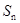 =
=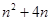 (
(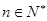 ), 数列
), 数列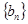 为等比数列,首项
为等比数列,首项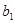 =2,公比为q(q>0)且满足
=2,公比为q(q>0)且满足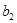 ,
,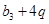 ,
,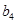 为等比数列.
为等比数列.
(1)求数列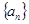 ,
,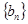 的通项公式;
的通项公式;
(2)设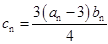 ,记数列
,记数列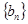 的前n项和为Tn,,求Tn。
的前n项和为Tn,,求Tn。
F1、F2为双曲线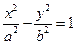 的左右焦点,O为坐标原点,P在双曲线的左支上,点M在右准线上,且满足:
的左右焦点,O为坐标原点,P在双曲线的左支上,点M在右准线上,且满足: ,
, (λ>0)
(λ>0)
(1)求此双曲线的离心率;
(2)若过点N( ,
,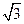 )的双曲线C的虚轴端点分别为B1、B2(B1在y轴正半轴上),点A、B在双曲线上,且
)的双曲线C的虚轴端点分别为B1、B2(B1在y轴正半轴上),点A、B在双曲线上,且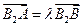 ,
, ,求双曲线C和直线AB的方程。
,求双曲线C和直线AB的方程。
已知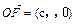 (c>0),
(c>0),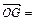 (n, n)(n∈R),
(n, n)(n∈R), 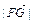 的最小值为1,若动点P同时满足下列三个条件:①
的最小值为1,若动点P同时满足下列三个条件:①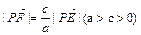 ,②
,② (其中
(其中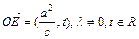 );③动点P的轨迹C经过点B(0,-1)。
);③动点P的轨迹C经过点B(0,-1)。
(1)求c值;(2)求曲线C的方程;(3)方向向量为 的直线l与曲线C交于不同两点M、N,若
的直线l与曲线C交于不同两点M、N,若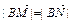 ,求k的取值范围。
,求k的取值范围。
在直角坐标平面中,△ABC的两个顶点为 A(0,-1),B(0, 1)平面内两点G、M同时满足①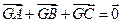 ,②
,②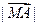 =
= 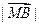 =
= 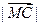 ③
③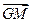 ∥
∥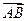
(1)求顶点C的轨迹E的方程
(2)设P、Q、R、N都在曲线E上 ,定点F的坐标为(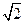 , 0) ,已知
, 0) ,已知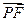 ∥
∥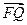 ,
,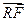 ∥
∥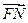 且
且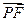 ·
·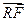 = 0.求四边形PRQN面积S的最大值和最小值.
= 0.求四边形PRQN面积S的最大值和最小值.
(本小题满分13分)如图,在直三棱柱ABC—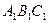 中,
中,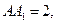 AB = 1,
AB = 1, ;点D、E分别在
;点D、E分别在 上,且
上,且 ,
,
四棱锥 与直三棱柱的体积之比为3:5。
与直三棱柱的体积之比为3:5。
(1)求异面直线DE与 的距离;(8分)
的距离;(8分)
(2)若BC = ,求二面角
,求二面角 的平面角的正切值。(5分)
的平面角的正切值。(5分)
|
(本小题满分13分)某单位有三辆汽车参加某种事故保险,单位年初向保险公司
缴纳每辆900元的保险金.对在一年内发生此种事故的每辆汽车,单位获9000元
的赔偿(假设每辆车最多只赔偿一次)。设这三辆车在一年内发生此种事故的概率
分别为 且各车是否发生事故相互独立,求一年内该单位在此保险中:
且各车是否发生事故相互独立,求一年内该单位在此保险中:
(1)获赔的概率;(4分)
(2)获赔金额 的分别列与期望。(9分)
的分别列与期望。(9分)