(本小题满分13分)如图，在直三棱柱ABC—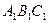
中，
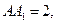AB = 1,
；点D、E分别在
上，且
，
四棱锥
与直三棱柱的体积之比为3：5。
（1）求异面直线DE与
的距离；(8分)
（2）若BC =
，求二面角
的平面角的正切值。(5分)
|
求过点
且与椭圆
有相同焦点
的椭圆标准方程解。
已知函数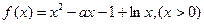
（1）当
时，求
的单调递增区间;
（2）若在
上是增函数，求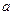
的取值范围;
（3）是否存在实数
使得方程
在区间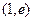
上有解，若存在，
试求出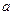的取值范围，若不存在，请说明理由.
已知抛物线
，点
为坐标原点，斜率为1的
直线与抛物线交于
两点
（1）若直线
过点
且
，求
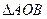的面积;
（2）若直线过抛物线的焦点且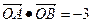
，求抛物线的方程.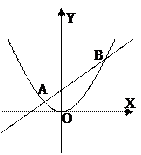
如图，有一块抛物线形钢板，其下口宽为 2 米 ，高为 2米.计划将此钢板
切割成等腰梯形的形状，下底AB是抛物线的下口，上底CD的端点在抛物线上，
(1) 请建立适当的直角坐标系，求抛物线形钢板所在抛物线方程;
（2）记CD =" 2" x ，写出梯形面积S 以 x 为自变量的函数式，并指出定义域;
（3）求面积S的最大值.
 |
（本小题满分10分）
已知函数
在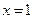
处的切线方程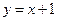
（1）求a，b的值；
（2）求函数
在 
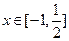值域.
