在直角坐标平面中,△ABC的两个顶点为 A(0,-1),B(0, 1)平面内两点G、M同时满足①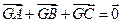 , ②
, ②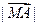 =
= 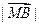 =
= 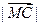 ③
③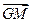 ∥
∥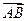
(1)求顶点C的轨迹E的方程
(2)设P、Q、R、N都在曲线E上 ,定点F的坐标为(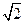 , 0) ,已知
, 0) ,已知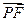 ∥
∥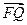 ,
,
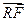 ∥
∥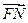 且
且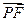 ·
·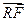 = 0.求四边形PRQN面积S的最大值和最小值.
= 0.求四边形PRQN面积S的最大值和最小值.
如图,四棱锥P-ABCD的底面是正方形,PD 面ABCD,E是PD上一点.
面ABCD,E是PD上一点.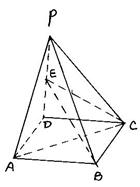
(1)求证:AC BE.
BE.
(2)若PD=AD=1,且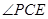 的余弦值为
的余弦值为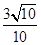 ,求三棱锥E-PBC的体积.
,求三棱锥E-PBC的体积.
已知 ,
,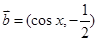 ,若
,若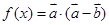 ,求:
,求:
(1)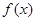 的最小正周期及对称轴方程.
的最小正周期及对称轴方程.
(2)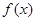 的单调递增区间.
的单调递增区间.
(3)当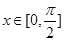 时,函数
时,函数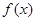 的值域.
的值域.
已知函数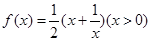 ,
,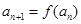 ,对于任意的
,对于任意的 ,都有
,都有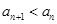 .
.
(1)求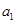 的取值范围
的取值范围
(2)若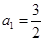 ,证明:
,证明: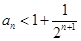 (
(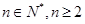 )
)
(3)在(2)的条件下,证明:
如图,直角坐标系XOY中,点F在x轴正半轴上,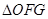 的面积为S.且
的面积为S.且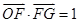 ,设
,设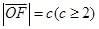 ,
, .
.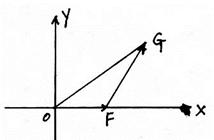
(1)以O为中心,F为焦点的椭圆E经过点G,求点G的纵坐标.
(2)在(1)的条件下,当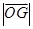 取最小值时,求椭圆E的标准方程.
取最小值时,求椭圆E的标准方程.
(3)在(2)的条件下,设点A、B分别为椭圆E的左、右顶点,点C是椭圆的下顶点,点P在椭圆E上(与点A、B均不重合),点D在直线PA上,若直线PB的方程为 ,且
,且 ,试求CD直线方程.
,试求CD直线方程.
已知函数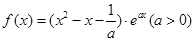
(1)当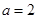 时,求函数
时,求函数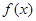 的单调区间.
的单调区间.
(2)若不等式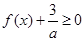 对任意的
对任意的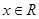 恒成立,求a的取值范围.
恒成立,求a的取值范围.