如图所示,边长为L的正方形金属框,质量为m,电阻为R,用细线把它悬挂于一个有界的匀强磁场边缘,金属框的上半部处于磁场内,下半部处于磁场外.磁场随时间变化规律为B=kt(k>0),已知细线所能承受的最大拉力为2mg,求:
(1)回路中的感应电流大小及方向
(2)从t=0开始,经多长时间细线会被拉断
如图所示,已知半径分别为R和r的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,甲轨道左侧又连接一个光滑的轨道,两圆形轨道之间由一条水平轨道 CD相连.一小球自某一高度由静止滑下,先滑上甲轨道,通过动摩擦因数为μ的CD段,又滑上乙轨道,最后离开两圆轨道.若小球在两圆轨道的最高点对轨道压 力都恰好为零.试求:⑴分别经过C、D时的速度;⑵小球释放的高度h; ⑶水平CD段的长度.
一宇航员抵达一半径为R的星球表面后,为了测定该星球的质量M,做如下实验,取一根细线穿过光滑的细直管,细线一端栓一质量为m的砝码,另一端连在一固定的测力计上,手握细直管抡动砝码,使它在竖直平面内做完整的圆周运动。停止抡动细直管,砝码可继续在同一竖直平面做完整的圆周运动。如图所示,观察测力计得到,当砝码运动到圆周的最低点时,测力计的读数为 ;当砝码运动到圆周的最高点时,测力计的读数为
;当砝码运动到圆周的最高点时,测力计的读数为 。已知引力常量为G,试根据题中提供的条件和测量结果,求:
。已知引力常量为G,试根据题中提供的条件和测量结果,求:
(1)该星球表面的重力加速度;
(2)该星球的质量M;
(3)该星球的第一宇宙速度。
如图所示,水平台面AB距地面的高度h=0.80m.有一滑块从A点以v0 =6.0m/s的初速度在台面上做匀变速直线运动,滑块与平台间的动摩擦因数μ=0.5.滑块运动到平台边缘的B点后水平飞出.已知AB=2.7m。不计空气阻力,g取10m/s2,求:
(1)滑块从B点飞出时的速度大小;
(2)滑块落地点到平台边缘的水平距离;
(3)滑块落地前瞬间的速度与水平方向的夹角(结果可直接用三角函数表示)。
如图所示,一带电为+q质量为m的小球,从距地面高h处以一定的初速水平抛出,在距抛出点水平距离为L处有根管口比小球略大的竖直细管,管的上口距地面h/2。为了使小球能无碰撞地通过管子(即以竖直速度进入管子),可在管子上方整个区域内加一水平向左的匀强电场,求: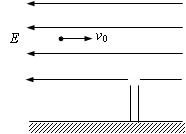
(1)小球的初速度
(2)应加电场的场强
(3)小球落地时的动能
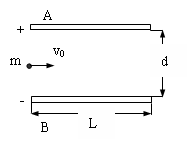
两平行金属板A、B水平放置,一个质量为m=5×10-6kg的带电微粒以v0=2m/s的水平速度从两板正中位置射入电场,如图所示,A、B 间距为d=4cm,板长L= 10cm. (g取10m/s2)
(1)当A、B间电压UAB=1.0×103V时,微粒恰好不发生偏转,求该微粒的 电性和电荷量.
电性和电荷量.
(2)要使用粒子恰好能从A板边缘飞出,求AB两板的电 势差
势差