一块直角三角板XYZ放置在△ABC上,三角板XYZ的两条直角边XY、XZ恰好分别经过点B、C.△ABC中,∠A=50°.
(1)如图1,则∠ABC+∠ACB= 度,∠XBC+∠XCB= 度;
(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过点B、C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.
(8分)比较正五边形与正六边形,可以发现它们的相同点和不同点.例如: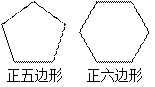
它们的一个相同点:正五边形的各边相等,正六边形的各边也相等.
它们的一个不同点:正五边形不是中心对称图形,正六边形是中心对称图形.
请你再写出它们的两个相同点和不同点:
相同点:
① ;
② .
不同点:
① ;
② .
(8分)在社区全民健身活动中,父子俩参加跳绳比赛.相同时间内父亲跳180个,儿子跳210个.已知儿子每分钟比父亲多跳20个,父亲、儿子每分钟各跳多少个?
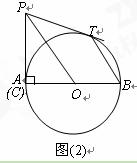
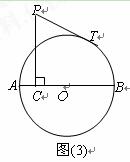
已知,AB是⊙O的直径,AB=8,点C在⊙O的半径OA上运动,PC⊥AB,垂足为C,PC=5,PT为⊙O的切线,切点为T.
⑴如图⑴,当C点运动到O点时,求PT的长;
⑵如图⑵,当C点运动 到A点时,连结PO、BT,求证:PO∥BT;
到A点时,连结PO、BT,求证:PO∥BT;
⑶如图⑶,设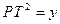 ,
,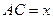 ,求
,求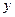 与
与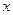 的函数关系式及
的函数关系式及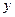 的
的 最小值.
最小值.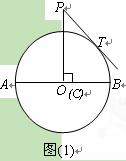
如图,直线 交
交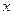 轴于A点,交
轴于A点,交 轴于B点,过A、B两点的抛物线交
轴于B点,过A、B两点的抛物线交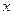 轴于另一点C(3,0)
轴于另一点C(3,0) .
.
⑴求抛物线的解析式;
⑵在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
两个全等的直角三角形重叠放在直线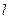 上,如图⑴,AB=6
上,如图⑴,AB=6 ,BC=8
,BC=8 ,∠ABC=90°,将Rt△ABC在直线
,∠ABC=90°,将Rt△ABC在直线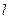 上左右平移,如图⑵所示.
上左右平移,如图⑵所示.
⑴求证:四边形ACFD是平行四边形;
⑵怎样移动Rt△ABC,使得四边形ACFD为菱形;
⑶将Rt△ABC向左平移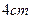 ,求四边形DHCF的面积.
,求四边形DHCF的面积.