如图(1)，点A、B、C在同一直线上，且△ABE, △BCD都是等边三角形，连结AD,CE.
(1)△BEC可由△ABD顺时针旋转得到吗？若是，请描述这一旋转变换过程；若不是，请说明理由；
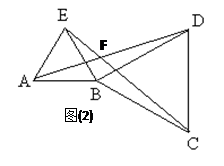
(2)若△BCD绕点B顺时针旋转，使点A,B,C不在同一直线上（如图(2)），则在旋转过程中:
①线段AD与EC的长度相等吗？请说明理由．
②锐角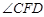
的度数是否改变？若不变，请求出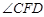的度数；若改变，请说明理由.
(注:等边三角形的三条边都相等,三个角都是60°)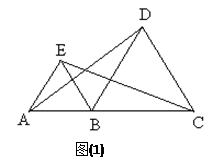
如图9，△ABC是等边三角形，D点是AC的中点，延长BC到E，使CE=CD.
（1）用尺规作图的方法，过D点作DF⊥BE，垂足是F（不写作法，保留作图痕迹）；
（2）求证：BF=EF．
某市今年计划修建一段全长1500米的景观路，为了尽量减少施工对城市交通的影响，实际施工时，每天的工效比原计划增加20%，结果提前2天完成这一任务，求原计划每天修路多少米？
计算（第（1）小题3分，第（2）小题6分，共9分）
（1）
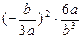；（2）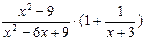
.
如图9，在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上，且AB=3,AD=2,经过点C的直线y=x-2与x轴、y轴分别交于点E、F.
（1）求矩形ABCD的顶点A、B、C、D的坐标；
（2）求证：△OEF≌△BEC；
（3）P为直线y=x-2上一点，若S△POE=5，求点P的坐标.
（10分)如图8, △ABC是等边三角形，D是BC延长线上任意一点，以AD为一边向右侧作等边△ADE，连接CE.
（1）求证：△CAE≌△BAD；
（2）判断直线AB与EC的位置关系，并说明理由.