(本小题满分10分)如图,AB//CD,∠B=75°,∠D=40°,求∠F的度数?

如图,已知△ABC和△DEF是两个边长都为10cm的等边三角形,且B、D、C、E都在同一条直线上,连接AD、CF.
(1)求证:四边形ADFC是平行四边形;
(2)若BD=3cm,△ABC沿着BE的方向以每秒1cm的速度运动,设△ABC运动的时间为t秒,
①当t为何值时,平行四边形ADFC是菱形?请说明理由;
②平行四边形ADFC有可能是矩形吗?若可能,求出t的值;若不可能,请说明理由。
在学校组织的知识竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在C级以上(包括C级)的人数为_______;
(2)请你将表格补充完整:
| 平均数 |
中位数 |
众数 |
|
| 一班 |
87.6 |
90 |
|
| 二班 |
87.6 |
100 |
(3)请从下列不同角度对这次竞赛成绩的结果进行分析:
①从平均数和中位数的角度来比较一班和二班的成绩;
②从平均数和众数的角度来比较一班和二班的成绩;
③从B级以上(包括B级)的人数的角度来比较一班和二班的成绩.
某气球内充满了一定质量的气体,当温度不变时,气球内的气压p(kpa)是气体体积V(m3)的反比例函数,其图象如图所示,当气球内的气压大于140kpa时,气球将会爆炸,为了安全,请你求出气体体积的范围.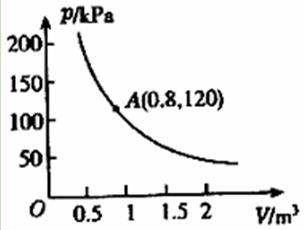
某人骑自行车的速度比步行的速度每小时多走8千米,已知步行12千米所用的时间和骑自行车36千米所用的时间相等,这个人步行每小时走多少千米?