“五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满500元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费500元.
(1)该顾客至多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
如图,点E是正方形ABCD的边AB上任意一点,过点D作DF⊥DE交BC的延长线于点F.求证:DE=DF.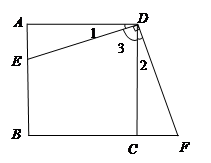
(6分)如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD.求该矩形草坪BC边的长.
如图1,在平面直角坐标系中, 为坐标原点.直线
为坐标原点.直线 与抛物线
与抛物线 同时经过
同时经过 .
.
(1)求 的值.
的值.
(2)点 是二次函数图象上一点,(点
是二次函数图象上一点,(点 在
在 下方),过
下方),过 作
作
 轴,与
轴,与 交于点
交于点 ,与
,与 轴交于点
轴交于点 .求
.求 的最大值.
的最大值.
(3)在(2)的条件下,是否存在点 ,使
,使 和
和  相似?若存在,求出
相似?若存在,求出 点坐标,不存在,说明理由.
点坐标,不存在,说明理由.
 中,AB=AC,将线段AB绕点A按逆时针方向旋转
中,AB=AC,将线段AB绕点A按逆时针方向旋转 得到线段AD,其中
得到线段AD,其中 .连结BD,CD,
.连结BD,CD,  .
.
(1)若 ,
, ,在图1中补全图形,并写出m值.
,在图1中补全图形,并写出m值.
(2)如图2,当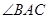 为钝角,
为钝角, 时 ,
时 , 值是否发生改变?证明你的猜想.
值是否发生改变?证明你的猜想.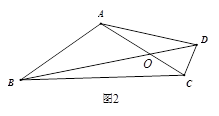
(3) 如图3,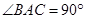 ,
, ,BD与AC相交于点O,求
,BD与AC相交于点O,求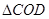 与
与 的面积比.
的面积比.
在平面直角坐标系 中,抛物线
中,抛物线 的开口向下,且抛物线与
的开口向下,且抛物线与 轴的交于点
轴的交于点 ,与
,与 轴交于
轴交于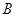 ,
, 两点,(
两点,(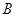 在
在 左侧). 点
左侧). 点 的纵坐标是
的纵坐标是 .
.
(1)求抛物线的解析式;
(2)求直线 的解析式;
的解析式;
(3)将抛物线在点 左侧的图形(含点
左侧的图形(含点 )记为
)记为 .若直线
.若直线 与直线
与直线 平行,且与
平行,且与
图形 恰有一个公共点,结合函数图象写出
恰有一个公共点,结合函数图象写出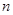 的取值范围.
的取值范围.