已知点P的坐标为（m，0），在x轴上存在点Q（不与P点重合），以PQ为边长作正方形PQMN，使点M落在反比例函数
的图像上．小明对上述问题进行了探究，发现不论m取何值，符合上述条件的正方形只有两个，且一个正方形的顶点M在第四象限，另一个正方形的顶点
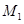在第二象限；
（1）如图所示，点P坐标为（1，0），图中已画出一个符合条件的正方形PQMN，请你在图中画出符合条件的另一个正方形
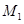，并写出点的坐标；
（2）请你通过改变P点的坐标，对直线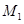M的解析式y﹦kx＋b进行探究：
①k= ；
②若点P的坐标为（m，0），则b= ；
（3）依据(2)的规律，如果点P的坐标为（8，0），请你求出点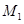和点M的坐标．
如图，已知△ABC中，AB=AC，AB边上的垂直平分线DE交BA于点D，交AC于点E.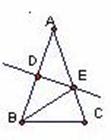
(1)若AB=8cm，△BCE的周长是14cm，求BC的长;
(2)若∠ABE：∠EBC＝2:1，求∠A的度数.
计算：
（1）
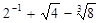（2）
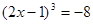
实践与探索:
㈠小明在玩积木游戏时，把三个正方形积木摆成一定的形状,正视图如图①,
问题(2):若P的面积为36cm2,Q的面积为64 cm2,同时M的面积为100 cm2,则△DEF为_______三角形。
㈡图形变化：Ⅰ.如图②,分别以直角三角形的三边为直径向三角形外作三个半圆,你能找出这三个半圆的面积之间有什么关系吗?请说明理由。
Ⅱ.如图③,如果直角三角形两直角边的长分别为3和4,以直角三角形的三边为直径作半圆,你能利用上面中的结论求出阴影部分的面积吗? 
如图，在△ABC中，∠BAC=90°，AB=AC，点D在BC上，且BD=BA，点E在BC的延长线上，且CE=CA。
(1)试求∠DAE的度数。
(2)如果把第（1）题中“AB=AC”的条件去掉，其余条件不变，那么∠DAE的度数会改变吗？试说明理由。
如图，一架云梯长25米，斜靠在一面墙上，梯子底端离墙7米。
（1）这个梯子的顶端距地面有多高？
（2）如果梯子的顶端下滑4米，那么梯子的底部在水平方向也滑动了4米吗？