如图,直线与轴,轴分别交于,两点,过,两点的抛物线与轴交于点.
(1)求抛物线的解析式;
(2)连接,若点是线段上的一个动点(不与,重合),过点作,交于点,当的面积是时,求点的坐标;
(3)在(2)的结论下,将绕点旋转得△,试判断点是否在抛物线上,并说明理由.

超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在A处,离益阳大道的距离(AC)为30米.这时,一辆小轿车由西向东匀速行驶,测得此车从B处行驶到C处所用的时间为8秒,∠BAC=75°.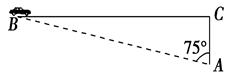
(1)求B、C两点的距离;
(2)请判断此车是否超过了益阳大道60千米/小时的限制速度?
(计算时距离精确到1米,参考数据:sin 75°≈0.965 9,cos 75°≈0.258 8,tan 75°≈3.732,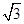 ≈1.732,60千米/小时≈16.7米/秒)
≈1.732,60千米/小时≈16.7米/秒)
如图,为了测量电线杆AB的高度,小明将测角仪放在与电线杆的水平距离为9 m的D处.若测角仪CD的高度为1.5 m,在C处测得电线杆顶端A的仰角为36°,则电线杆AB的高度约为________m(精确到0.1 m).(参考数据:sin 36°≈0.59,cos 36°≈0.81,tan 36°≈0.73)
如图在Rt△ABC中,∠ACB=90°,D是边AB的中点,BE⊥CD,垂足为点E.已知AC=15,cos A= .
.
(1)求线段CD的长;
(2)求sin ∠DBE的值.
如图,菱形ABCD和菱形ECGF的边长分别为2和3,∠A=120°,则图中阴影部分的面积是多少?
如图,在△ABC中,AD是BC边上的高,tan C= ,AC=3,AB=4,求BD的长.(结果保留根号)
,AC=3,AB=4,求BD的长.(结果保留根号)