已知：如图①，在矩形ABCD中，AB=5，AD=
，AE⊥BD，垂足是E．点F是点E关于AB的对称点，连接AF、BF．
（1）求AE和BE的长；
（2）若将△ABF沿着射线BD方向平移，设平移的距离为m（平移距离指点B沿BD方向所经过的线段长度）．当点F分别平移到线段AB．AD上时，直接写出相应的m的值．
（3）如图②，将△ABF绕点B顺时针旋转一个角α（0°＜α＜180°），记旋转中的△ABF为△A′BF′，在旋转过程中，设A′F′所在的直线与直线AD交于点P，与直线BD交于点Q．是否存在这样的P、Q两点，使△DPQ为等腰三角形？若存在，求出此时DQ的长；若不存在，请说明理由．
某学校后勤人员到一家文具店给九年级的同学购买考试用文具包，文具店规定一次购买400个以上，可享受8折优惠．若给九年级学生每人购买一个，不能享受8折优惠，需付款1936元；若多买88个，就可享受8折优惠，同样只需付款1936元．请问该学校九年级学生有多少人？
如图所示，△ABC是等边三角形，D是AC的中点，延长BC到E，使CE=CD．
（1）用尺规作图的方法，过D点作DM⊥BE，垂足是M（不写作法，保留作图痕迹）；
（2）求证：BM=EM．
已知反比例函数y=
（k≠0）的图象经过点
（3，2）．
（1）求这个函数的解析式；
（2）当－4＜x＜－1时，求y的取值范围．
计算：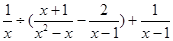
（满分14分）如图,抛物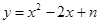线
与直线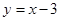
相交于A、B两点（点A在x轴上，点B在y轴上），与x轴的另一个交点为点C．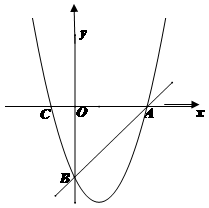
（1）求抛物线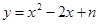
的解析式；
（2）在x轴下方，当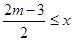
<
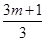时，抛物线y随x增大而减小，求实数m 的取值范围；
（3）在抛物线上，是否存在点F，使得△BCF是直角三角形？若存在，求出所有满足条件的点F的坐标；若不存在，请说明理由．