我校高三年级进行了一次水平测试.用系统抽样的方法抽取了50名学生的数学成绩,准备进行分析和研究.经统计成绩的分组及各组的频数如下:
[40,50), 2; [50,60), 3; [60,70), 10; [70,80), 15; [80,90), 12; [90,100], 8.
(Ⅰ)完成样本的频率分布表;画出频率分布直方图.
(Ⅱ)估计成绩在85分以下的学生比例;
(Ⅲ)请你根据以上信息去估计样本的众数、中位数、平均数.(精确到0.01)
(Ⅰ)频率分布表
| 分组 |
频数 |
频率 |
| [40,50) |
2 |
|
| [50,60) |
3 |
|
| [60,70) |
10 |
|
| [70,80) |
15 |
|
| [80,90) |
12 |
|
| [90,100] |
8 |
|
| 合计 |
50 |
|
(Ⅰ)频率分布直方图为
(本小题满分10分)选修4-4:坐标系与参数方程
曲线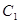 的参数方程为
的参数方程为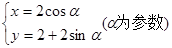 ,
,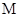 是曲线
是曲线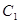 上的动点,且
上的动点,且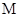 是线段
是线段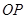 的中点,
的中点,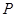 点的轨迹为曲线
点的轨迹为曲线 ,直线l的极坐标方程为
,直线l的极坐标方程为 ,直线l与曲线
,直线l与曲线 交于
交于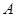 ,
,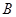 两点。
两点。
(Ⅰ)求曲线 的普通方程;
的普通方程;
(Ⅱ)求线段 的长。
的长。
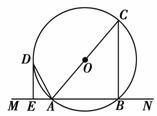
(本小题满分10分)选修4-1 :几何证明选讲
直线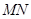 交圆
交圆 于
于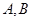 两点,
两点,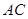 是直径,
是直径,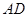 平分
平分 ,交圆
,交圆 于点
于点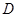 ,过
,过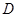 作
作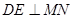 于
于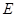 。
。
(Ⅰ)求证: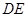 是圆
是圆 的切线;
的切线;
(Ⅱ)若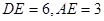 ,求
,求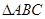 的面积。
的面积。
(本小题满分12分)已知函数 ,
,
(Ⅰ)求函数 的单调区间和极值;
的单调区间和极值;
(Ⅱ)若对任意的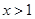 ,恒有
,恒有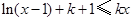 成立,求
成立,求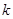 的取值范围;
的取值范围;
(Ⅲ)证明: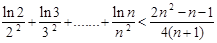 (
(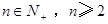 ).
).
(本小题满分12分)已知椭圆C: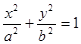 (a>b>0)与y轴的交点为A,B(点A位于点B的上方),F为左焦点,原点O到直线FA的距离为
(a>b>0)与y轴的交点为A,B(点A位于点B的上方),F为左焦点,原点O到直线FA的距离为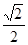 b.
b.
(Ⅰ)求椭圆C的离心率;
(Ⅱ)设b=2,直线y=kx+4与椭圆C交于不同的两点M,N,求证:直线BM与直线AN的交点G在定直线上.
(本小题满分12分)如图,四棱锥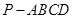 ,侧面
,侧面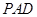 是边长为
是边长为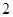 的正三角形,且与底面垂直,底面
的正三角形,且与底面垂直,底面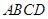 是
是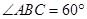 的菱形,
的菱形, 为
为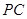 的中点.
的中点.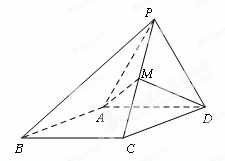
(Ⅰ)求证: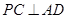 ;
;
(Ⅱ)求点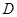 到平面
到平面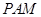 的距离.
的距离.