如图,为了测量河对岸A、B两点之间的距离,观察者找到一个点C,从C点可以观察到点A、B;找到一个点D,从D点可以观察到点A、C:找到一个点E,从E点可以观察到点B、C。并测得以下数据:CD=CE=100m,∠ACD=90°,∠ACB=45°,∠BCE=75°,∠CDA=∠CEB=60°,求A、B两 点之间的距离。
已知函数 ,曲线
,曲线 在点
在点 处的切线与
处的切线与 轴交点的横坐标为
轴交点的横坐标为 .
.
(1)求 ;
;
(2)证明:当 时,曲线
时,曲线 与直线
与直线 只有一个交点.
只有一个交点.
设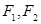 分别是椭圆
分别是椭圆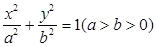 的左右焦点,
的左右焦点,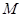 是
是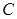 上一点且
上一点且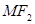 与
与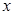 轴垂直,直线
轴垂直,直线 与
与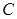 的另一个交点为
的另一个交点为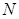 .
.
(1)若直线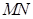 的斜率为
的斜率为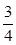 ,求
,求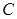 的离心率;
的离心率;
(2)若直线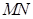 在
在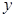 轴上的截距为
轴上的截距为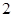 ,且
,且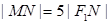 ,求
,求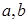 .
.
如图,四棱锥 中,底面
中,底面 为矩形,
为矩形,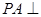 平面
平面 ,
,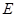 是
是 的中点.
的中点.
(1)证明: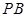 //平面
//平面 ;
;
(2)设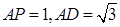 ,三棱锥
,三棱锥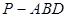 的体积
的体积 ,求
,求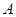 到平面
到平面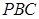 的距离.
的距离.
某公司为了了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对其产品的满意度的评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频率分布表.
A地区用户满意度评分的频率分布直方图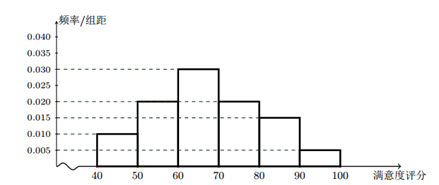
B地区用户满意度评分的频率分布表
| 满意度评分分组 |
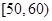 |
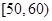 |
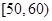 |
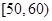 |
 |
| 频数 |
2 |
8 |
14 |
10 |
6 |
(Ⅰ)作出B地区用户满意度评分的频率分布直方图,并通过此图比较两地区满意度评分的平均值及分散程度.(不要求计算出具体值,给出结论即可)
B地区用户满意度评分的频率分布直方图
(Ⅱ)根据用户满意度评分,将用户的满意度评分分为三个等级:
| 满意度评分 |
低于70分 |
70分到89分 |
不低于90分 |
| 满意度等级 |
不满意 |
满意 |
非常满意 |
估计那个地区的用户的满意度等级为不满意的概率大,说明理由.
已知等差数列{an}的公差不为零,a1=25,且 ,
,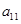 ,
,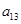 成等比数列.
成等比数列.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)求 +a4+a7+…+a3n-2.
+a4+a7+…+a3n-2.