已知抛物线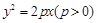
的焦点为
，点
是抛物线上的一点，且其纵坐标为4，
．
（1）求抛物线的方程；
（2） 设点
是抛物线上的两点，
的角平分线与
轴垂直，求
的面积最大时直线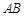
的方程．
将一颗质地均匀的正方体骰子（六个面的点数分别为1，2，3，4，5，6）先后抛掷两次，将得到的点数分别记为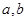
.
（1）求直线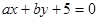
与圆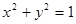
相切的概率；
（2）将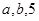
的值分别作为三条线段的长，求这三条线段能围成等腰三角形的概率．
已知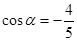
，求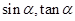
求圆心在直线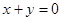
上，且过两圆
，
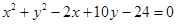交点的圆的方程．
某公交公司为了估计某线路公交公司发车的时间间隔，对乘客在这条线路上的某个公交车站等车的时间进行了调查，以下是在该站乘客候车时间的部分记录：
| 等待时间（分钟） |
频数 |
频率 |
| ［0，3） |
0.2 |
|
| ［3，6） |
0.4 |
|
| ［6，9） |
5 |
x |
| ［9，12） |
2 |
y |
| ［12，15） |
1 |
0.05 |
| 合计 |
z |
1 |
求（1）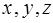
；
（2）画出频率分布直方图；
（3）计算乘客平均等待时间的估计值。
（1）求三角函数cos(－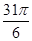
)的值.
（2）用三角函数线求函数y＝
的定义域．
（3）求函数y＝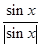
＋
＋
的值域．