如图所示，二次函数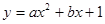
（
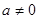）的图像与
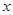轴分别交于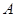
（
，
）、
（
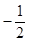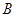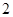，）两点，且与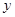
轴交于点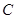
；
（1）求该拋物线的解析式，并判断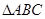
的形状；
（2）在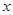轴上方的拋物线上有一点
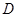，且以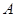、、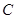、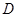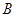四点为顶点的四边形是等腰梯形，请直接写
出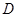点的坐标；
（3）在此拋物线上是否存在点P，使得以、、、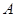
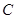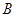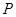四点为顶点的四边形是直角梯形？若存在，求
（4）出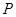点的坐标；若不存在，说明理由．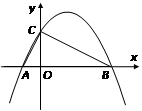
如图所示，AB⊥BC，DC⊥AC，垂足分别为B，C，过D点作BC的垂线交BC于F，交AC于E，AB=EC，试判断AC和ED的长度有什么关系并说明理由．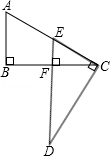
如图，AD平分∠BAC，DE⊥AB于E，DF⊥AC于F，且DB=DC，求证：EB=FC．
（1）如图1，△ABC中，∠BAC=90°，AB=AC，AE是过A点的一条直线，且B、C在AE的异侧，BD⊥AE于D，CE⊥AE于E，求证：BD=DE+CE．
（2）若直线AE绕点A旋转到图2的位置时（BD＜CE），其余条件不变，问BD与DE、CE的关系如何？请予以证明．
如图，∠A=∠B=90°，E是AB上的一点，且AE=BC，∠1=∠2．
（1）Rt△ADE与Rt△BEC全等吗？并说明理由；
（2）△CDE是不是直角三角形？并说明理由．
如图，已知在△ABC中，AB=AC，∠BAC=90°，分别过B、C向过A的直线作垂线，垂足分别为E、F．
（1）如图①过A的直线与斜边BC不相交时，求证：EF=BE+CF；
（2）如图②过A的直线与斜边BC相交时，其他条件不变，若BE=10，CF=3，求：FE长．