现有4个同学去看电影,他们坐在了同一排,且一排有6个座位.问:
(1)所有可能的坐法有多少种?
(2)此4人中甲,乙两人相邻的坐法有多少种?
(3)所有空位不相邻的坐法有多少种?(结果均用数字作答)
(本小题满分13分)已知定义在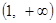 上的函数
上的函数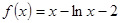 ,
,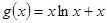 .
.
(1)求证: 存在唯一的零点,且零点属于(3,4);
存在唯一的零点,且零点属于(3,4);
(2)若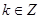 且
且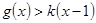 对任意的
对任意的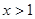 恒成立,求
恒成立,求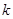 的最大值.
的最大值.
(本小题满分14分)如图,已知椭圆 的左焦点为F(
的左焦点为F( ,0),过点M(-3,0)作一条斜率大于0的直线
,0),过点M(-3,0)作一条斜率大于0的直线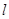 与椭圆W交于不同的两点A、B,延长BF交椭圆W于点C.
与椭圆W交于不同的两点A、B,延长BF交椭圆W于点C.
(1)求椭圆W的离心率;
(2)若∠MAC=60°,求直线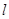 的斜率.
的斜率.
(本小题满分13分)设集合 ,从S的所有非空子集中,等可能地取出一个.
,从S的所有非空子集中,等可能地取出一个.
(1)设 ,若
,若 ,则
,则 ,就称子集A满足性质
,就称子集A满足性质 ,求所取出的非空子集满足性质
,求所取出的非空子集满足性质 的概率;
的概率;
(2)所取出的非空子集的最大元素为 ,求
,求 的分布列和数学期望
的分布列和数学期望 .
.
(本小题满分13分)如图,四棱锥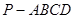 中,PA⊥平面ABCD,∠ABC=∠BAD=90°,AD=2PA=2AB=2BC=2.
中,PA⊥平面ABCD,∠ABC=∠BAD=90°,AD=2PA=2AB=2BC=2.
(1)求三棱锥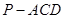 的外接球的体积;
的外接球的体积;
(2)求二面角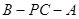 与二面角
与二面角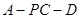 的正弦值之比.
的正弦值之比.
(本小题满分13分)在△ABC中,角A,B,C所对的边分别为 ,满足
,满足 ,且
,且 .
.
(1)求C的大小;
(2)求 的最大值,并求取得最大值时角A,B的值.
的最大值,并求取得最大值时角A,B的值.