在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北30°东,俯角为30°的B处,到11时10分又测得该船在岛北60°西、俯角为60°的C处。
(1)求船的航行速度是每小时多少千米;
(2)又经过一段时间后,船到达海岛的正西方向的D处,问此时船距岛A有多远?
(本小题满分12分)已知函数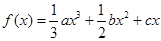 .(
.( )
)
(1)若函数 有三个零点
有三个零点 ,且
,且 ,
, ,求函数
,求函数 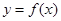 的单调区间;
的单调区间;
(2)若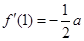 ,
, ,试问:导函数
,试问:导函数 在区间(0,2)内是否有零点,并说明理由.
在区间(0,2)内是否有零点,并说明理由.
(3)在(Ⅱ)的条件下,若导函数 的两个零点之间的距离不小于
的两个零点之间的距离不小于 ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)已知椭圆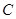 :
: (
(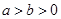 )的离心率为
)的离心率为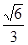 ,过右焦点
,过右焦点 且斜率为1的直线交椭圆
且斜率为1的直线交椭圆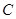 于
于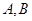 两点,
两点,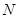 为弦
为弦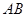 的中点。
的中点。
(1)求直线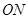 (
(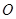 为坐标原点)的斜率
为坐标原点)的斜率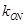 ;
;
(2)设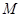 椭圆
椭圆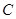 上任意一点,且
上任意一点,且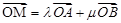 ,求
,求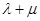 的最大值和最小值.
的最大值和最小值.
(本小题满分12分)已知直三棱柱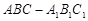 中,△
中,△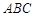 为等腰直角三角形,∠
为等腰直角三角形,∠ =
=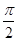 ,且
,且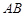 =
=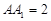 ,
,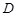 、
、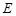 、
、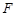 分别为
分别为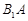 、
、 、
、 的中点.
的中点.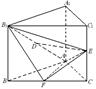
(1)求证: ∥平面
∥平面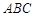 ;
;
(2)求证: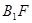 ⊥平面
⊥平面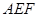 ;
;
(3)求三棱锥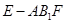 的体积.
的体积.
(本小题满分12分)设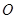 为坐标原点,点
为坐标原点,点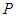 的坐标
的坐标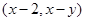
(1)在一个盒子中,放有标号为 的三张卡片,现从此盒中有放回地先后抽到两张卡片的标号分别记为
的三张卡片,现从此盒中有放回地先后抽到两张卡片的标号分别记为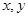 ,求|
,求|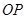 |的最大值,并求事件“|
|的最大值,并求事件“|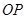 |取到最大值”的概率;
|取到最大值”的概率;
(2)若利用计算机随机在[ ,
,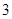 ]上先后取两个数分别记为
]上先后取两个数分别记为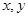 ,
,
求: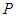 点在第一象限的概率.
点在第一象限的概率.
(本小题满分12分)如图: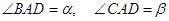 ,
,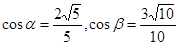 .
.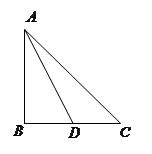
(1)求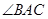 的大小;
的大小;
(2)当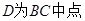 时,判断
时,判断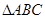 的形状,并求
的形状,并求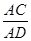 的值.
的值.