(本小题满分12分)设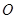 为坐标原点,点
为坐标原点,点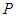 的坐标
的坐标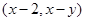
(1)在一个盒子中,放有标号为 的三张卡片,现从此盒中有放回地先后抽到两张卡片的标号分别记为
的三张卡片,现从此盒中有放回地先后抽到两张卡片的标号分别记为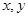 ,求|
,求|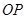 |的最大值,并求事件“|
|的最大值,并求事件“|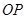 |取到最大值”的概率;
|取到最大值”的概率;
(2)若利用计算机随机在[ ,
,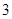 ]上先后取两个数分别记为
]上先后取两个数分别记为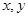 ,
,
求: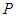 点在第一象限的概率.
点在第一象限的概率.
在平面直角坐标系 中,以坐标原点
中,以坐标原点 为极点,
为极点,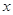 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线 的极坐标方程为
的极坐标方程为 ,直线
,直线 的参数方程为
的参数方程为 为参数,
为参数, ).
).
(1)化曲线 的极坐标方程为直角坐标方程;
的极坐标方程为直角坐标方程;
(2)若直线 经过点
经过点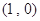 ,求直线
,求直线 被曲线
被曲线 截得的线段
截得的线段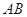 的长.
的长.
(已知矩阵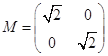 ,记绕原点逆时针旋转
,记绕原点逆时针旋转 的变换所对应的矩阵为
的变换所对应的矩阵为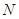
(1)求矩阵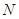 ;
;
(2)若曲线 :
: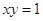 在矩阵
在矩阵 对应变换作用下得到曲线
对应变换作用下得到曲线 ,求曲线
,求曲线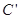 的方程.
的方程.
已知函数
(1)当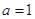 时,求函数
时,求函数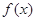 的极小值;
的极小值;
(2)当 时,过坐标原点
时,过坐标原点 作曲线
作曲线 的切线,设切点为
的切线,设切点为 ,求实数
,求实数 的值;
的值;
(3)设定义在 上的函数
上的函数 在点
在点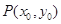 处的切线方程为
处的切线方程为 当
当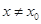 时,若
时,若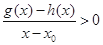 在
在 内恒成立,则称
内恒成立,则称 为函数
为函数 的“转点”.当
的“转点”.当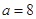 时,试问函数
时,试问函数 是否存在“转点”.若存在,请求出“转点”的横坐标,若不存在,请说明理由.
是否存在“转点”.若存在,请求出“转点”的横坐标,若不存在,请说明理由.
已知椭圆 :
: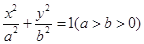 的左焦点为
的左焦点为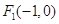 ,且过点
,且过点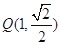 .
.
(1)求椭圆 的方程;
的方程;
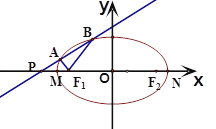
(2)设过点P(-2,0)的直线与椭圆E交于A、B两点,且满足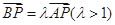 .
.
①若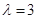 ,求
,求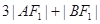 的值;
的值;
②若M、N分别为椭圆E的左、右顶点,证明: 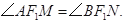
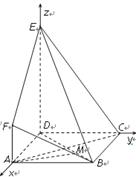
如图,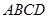 是边长为
是边长为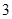 的正方形,
的正方形,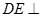 平面
平面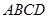 ,
,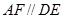 ,
,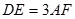 ,
,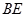 与平面
与平面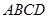 所成角为
所成角为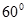 .
.
(1)求证: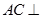 平面
平面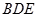 ;
;
(2)求二面角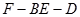 的余弦值;
的余弦值;
(3)设点 是线段
是线段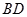 上一个动点,试确定点
上一个动点,试确定点 的位置,使得
的位置,使得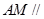 平面
平面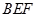 ,并证明你的结论.
,并证明你的结论.