已知函数
(1)当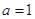 时,求函数
时,求函数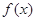 的极小值;
的极小值;
(2)当 时,过坐标原点
时,过坐标原点 作曲线
作曲线 的切线,设切点为
的切线,设切点为 ,求实数
,求实数 的值;
的值;
(3)设定义在 上的函数
上的函数 在点
在点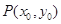 处的切线方程为
处的切线方程为 当
当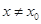 时,若
时,若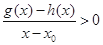 在
在 内恒成立,则称
内恒成立,则称 为函数
为函数 的“转点”.当
的“转点”.当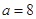 时,试问函数
时,试问函数 是否存在“转点”.若存在,请求出“转点”的横坐标,若不存在,请说明理由.
是否存在“转点”.若存在,请求出“转点”的横坐标,若不存在,请说明理由.
已知在 中,
中, ,且
,且 与
与 是方程
是方程 的两个根.
的两个根.
(Ⅰ)求 的值;
的值;
(Ⅱ)若 ,求
,求 的长.
的长.
如图,
四点在同一圆上,
的延长线与
的延长线交于
点,且
. 
(I)证明:
;
(II)延长
到
,延长
到
,使得
,证明:四点共圆.
在平面直角坐标系xoy中,已知曲线C1:x2+y2=1,以平面直角坐标系xoy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:ρ(2cosθ-sinθ)=6.
(Ⅰ)将曲线C1上的所有点的横坐标,纵坐标分别伸长为原来的 、2倍后得到曲线C2,试写出直线l的直角坐标方程和曲线C2的参数方程.
、2倍后得到曲线C2,试写出直线l的直角坐标方程和曲线C2的参数方程.
(Ⅱ)在曲线C2上求一点P,使点P到直线l的距离最大,并求出此最大值.
已知函数
(Ⅰ)解不等式: ;
;
(Ⅱ)当 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
如图,直线 经过⊙
经过⊙ 上的点
上的点 ,并且
,并且 ⊙
⊙ 交直线
交直线 于
于 ,
, ,连接
,连接 .
.
(I)求证:直线 是⊙
是⊙ 的切线;
的切线;
(II)若 ⊙
⊙ 的半径为
的半径为 ,求
,求 的长.
的长.