给定椭圆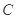 :
: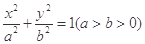 ,称圆心在原点
,称圆心在原点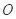 ,半径为
,半径为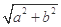 的圆是椭圆
的圆是椭圆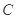 的“准圆”.若椭圆
的“准圆”.若椭圆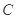 的一个焦点为
的一个焦点为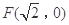 ,其短轴上的一个端点到
,其短轴上的一个端点到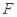 的距离为
的距离为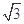 .
.
(1)求椭圆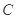 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(2)点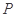 是椭圆
是椭圆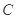 的“准圆”上的动点,过点
的“准圆”上的动点,过点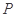 作椭圆的切线
作椭圆的切线 交“准圆”于点
交“准圆”于点 .
.
(ⅰ)当点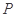 为“准圆”与
为“准圆”与 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线 的方程并证明
的方程并证明 ;
;
(ⅱ)求证:线段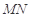 的长为定值.
的长为定值.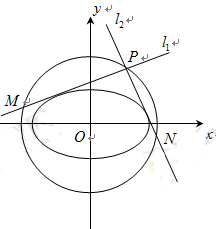
某厂家准备在2013年12月份举行促销活动,依以往的数据分析,经测算,该产品的年销售量 万件(假设该厂生产的产品全部销售),与年促销费用
万件(假设该厂生产的产品全部销售),与年促销费用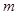 万元
万元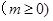 近似满足
近似满足 ,如果不促销,该产品的年销售量只能是1万件.已知2013年生产该产品的固定投入10万元,每生产1万件该产品需要再投入16万元.厂家将每件产品的销售价格规定为每件产品成本的1.5倍.(产品成本包括固定投入和再投入两部分资金).
,如果不促销,该产品的年销售量只能是1万件.已知2013年生产该产品的固定投入10万元,每生产1万件该产品需要再投入16万元.厂家将每件产品的销售价格规定为每件产品成本的1.5倍.(产品成本包括固定投入和再投入两部分资金).
(1)将2013年该产品的年利润 万元表示为年促销费用
万元表示为年促销费用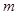 万元的函数;
万元的函数;
(2)该厂家2013年的年促销费用投入为多少万元时,该厂家的年利润最大?并求出年最大利润.
已知公差不为零的等差数列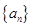 的前3项和
的前3项和 ,且
,且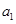 、
、 、
、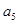 成等比数列.
成等比数列.
(1)求数列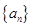 的通项公式及前n项的和
的通项公式及前n项的和 ;
;
(2)设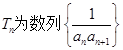 的前n项和,证明:
的前n项和,证明: ;
;
(3)对(2)问中的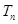 ,若
,若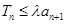 对一切
对一切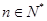 恒成立,求实数
恒成立,求实数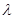 的最小值.
的最小值.
如图,已知在侧棱垂直于底面的三棱柱 中,
中,
 ,且
,且 ,点
,点 是
是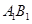 中点.
中点.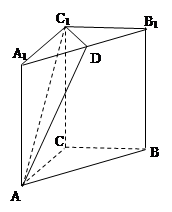
(1)求证:平面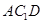 ⊥平面
⊥平面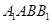 ;
;
(2)若直线 与平面
与平面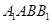 所成角的正弦值为
所成角的正弦值为 ,
,
求三棱锥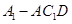 的体积.
的体积.
某高校从今年参加自主招生考试的学生中随机抽取容量为 的学生成绩样本,得到频率分布表如下:
的学生成绩样本,得到频率分布表如下:
| 组数 |
分组 |
频数 |
频率 |
| 第一组 |
[230,235) |
8 |
0.16 |
| 第二组 |
[235,240) |
 |
0.24 |
| 第三组 |
[240,245) |
15 |
 |
| 第四组 |
[245,250) |
10 |
0.20 |
| 第五组 |
[250,255] |
5 |
0.10 |
| 合计 |
 |
1.00 |
(1)求 的值;
的值;
(2)为了选拔出更加优秀的学生,该高校决定在第三、四、五组中用分层抽样的方法抽取6名学生进行第二轮考核,分别求第三、四、五组参加考核的人数;
(3)在(2)的前提下,高校决定从这6名学生中择优录取2名学生,求2人中至少有1人是第四组的概率.
设函数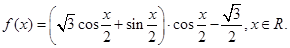
(1)求函数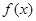 的最小正周期;
的最小正周期;
(2)记 的内角A、B、C的对边分别为
的内角A、B、C的对边分别为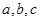 ,若
,若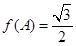 且
且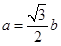 ,求角B的值.
,求角B的值.