某高校从今年参加自主招生考试的学生中随机抽取容量为 的学生成绩样本,得到频率分布表如下:
的学生成绩样本,得到频率分布表如下:
| 组数 |
分组 |
频数 |
频率 |
| 第一组 |
[230,235) |
8 |
0.16 |
| 第二组 |
[235,240) |
 |
0.24 |
| 第三组 |
[240,245) |
15 |
 |
| 第四组 |
[245,250) |
10 |
0.20 |
| 第五组 |
[250,255] |
5 |
0.10 |
| 合计 |
 |
1.00 |
(1)求 的值;
的值;
(2)为了选拔出更加优秀的学生,该高校决定在第三、四、五组中用分层抽样的方法抽取6名学生进行第二轮考核,分别求第三、四、五组参加考核的人数;
(3)在(2)的前提下,高校决定从这6名学生中择优录取2名学生,求2人中至少有1人是第四组的概率.
已知函数 成等差数列, 点
成等差数列, 点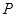 是函数
是函数 图像上任意一点,点
图像上任意一点,点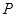 关于原点的对称点
关于原点的对称点 的轨迹是函数
的轨迹是函数 的图像
的图像
(1)解关于 的不等式
的不等式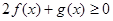 ;
;
(2)当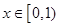 时,总有
时,总有 恒成立,求
恒成立,求 的取值范围.
的取值范围.
已知二次函数 的二次项系数为
的二次项系数为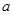 ,且不等式
,且不等式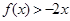 的解集为
的解集为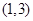 ,
,
(1)若方程 有两个相等的实根,求
有两个相等的实根,求 的解析式;
的解析式;
(2)若 的最大值为正数,求
的最大值为正数,求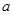 的取值范围.
的取值范围.
设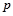 :实数
:实数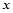 满足
满足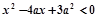 ,其中
,其中 ,
, :实数
:实数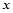 满足
满足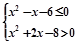 .
.
(1)若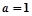 且
且 为真,求实数
为真,求实数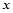 的取值范围;
的取值范围;
(2)若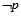 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数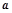 的取值范围.
的取值范围.
在△ABC中,角A,B,C的对边分别是a,b,c,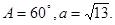 ,
,
(1)若 ,求
,求 的值.
的值.
(2)若△ABC是锐角三角形时,求 的取值范围。
的取值范围。
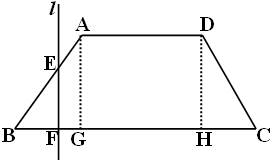
如图,已知底角为450的等腰梯形ABCD,底边BC长为7cm,腰长为 ,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式。
,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式。