某厂家准备在2013年12月份举行促销活动,依以往的数据分析,经测算,该产品的年销售量 万件(假设该厂生产的产品全部销售),与年促销费用
万件(假设该厂生产的产品全部销售),与年促销费用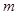 万元
万元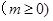 近似满足
近似满足 ,如果不促销,该产品的年销售量只能是1万件.已知2013年生产该产品的固定投入10万元,每生产1万件该产品需要再投入16万元.厂家将每件产品的销售价格规定为每件产品成本的1.5倍.(产品成本包括固定投入和再投入两部分资金).
,如果不促销,该产品的年销售量只能是1万件.已知2013年生产该产品的固定投入10万元,每生产1万件该产品需要再投入16万元.厂家将每件产品的销售价格规定为每件产品成本的1.5倍.(产品成本包括固定投入和再投入两部分资金).
(1)将2013年该产品的年利润 万元表示为年促销费用
万元表示为年促销费用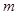 万元的函数;
万元的函数;
(2)该厂家2013年的年促销费用投入为多少万元时,该厂家的年利润最大?并求出年最大利润.
已知等比数列{an}的首项为a,公比为 q,其前n项和为Sn用a和q表示Sn,并证明你的结论.
如图,已知四棱锥P—ABCD中,底面ABCD是直角梯长,AB//CD,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1。
(1)求证:BC⊥平面PAC;
(2)若M是PC的中点,求三棱锥M—ACD的体积。
已知向量m=(cosx,sinx),n=(cosx,cosx)(x∈R),设函数f(x)=m·n
(1)求 f(x)的解析式,并求最小正周期.
(2)若函数 g(x)的图像是由函数 f(x)的图像向右平移 个单位得到的,求g(x)的最大值及使g(x)取得最大值时x的值.
个单位得到的,求g(x)的最大值及使g(x)取得最大值时x的值.
(本小题满分7分)选修4-5:不等式选讲
已知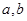 为正数,求证:
为正数,求证: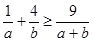 .
.
(本小题满分7分)选修4-4:坐标系与参数方程
在直角坐标系xoy中,直线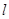 的参数方程为
的参数方程为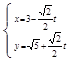 (t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为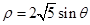 。
。
(1)求圆C的直角坐标方程;
(2)设圆C与直线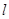 交于点A、B,若点P的坐标为
交于点A、B,若点P的坐标为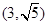 ,求|PA|+|PB|。
,求|PA|+|PB|。