在数列 中,
中, ,设
,设
(1)证明数列 是等差数列,并求其通项公式;
是等差数列,并求其通项公式;
(2)求所有正整数 的值,使得
的值,使得 中某个连续
中某个连续 项的和是数列
项的和是数列 中的第8项.
中的第8项.
(本小题满分12分)一个四棱锥的直观图和三视图如图所示: 

(1)求证: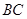 ⊥
⊥ ;
;
(2)求出这个几何体的体积。
(3)若在PC上有一点E,满足CE:EP=2:1,求证PA//平面BED。
已知直线 与圆
与圆 的交点为A、B,
的交点为A、B,
(1)求弦长AB;
(2)求过A、B两点且面积最小的圆的方程.
(本小题满分12分)
设函数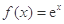 (
(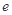 为自然对数的底数),
为自然对数的底数), (
(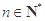 ).
).
(1)证明: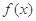
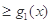 ;
;
(2)当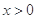 时,比较
时,比较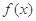 与
与 的大小,并说明理由;
的大小,并说明理由;
(3)证明: (
(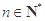 ).
).
(本小题满分12分)
已知数列 的相邻两项
的相邻两项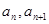 是关于
是关于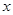 的方程
的方程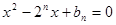
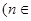 N
N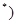 的两根,且
的两根,且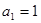 .
.
(1) 求数列 和
和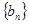 的通项公式;
的通项公式;
(2) 设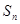 是数列
是数列 的前
的前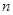 项和, 问是否存在常数
项和, 问是否存在常数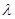 ,使得
,使得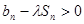 对任意
对任意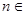 N
N 都成立,若存在, 求出
都成立,若存在, 求出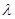 的取值范围; 若不存在, 请说明理由.
的取值范围; 若不存在, 请说明理由.
(本小题满分12分) 年中秋、国庆长假期间,由于国家实行
年中秋、国庆长假期间,由于国家实行 座及以下小型车辆高速公路免费政策,导致在长假期间高速公路出现拥堵现象。长假过后,据有关数据显示,某高速收费路口从上午
座及以下小型车辆高速公路免费政策,导致在长假期间高速公路出现拥堵现象。长假过后,据有关数据显示,某高速收费路口从上午 点到中午
点到中午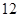 点,车辆通过该收费站的用时
点,车辆通过该收费站的用时 (分钟)与车辆到达该收费站的时刻
(分钟)与车辆到达该收费站的时刻 之间的函数关系式可近似地用以下函数给出:
之间的函数关系式可近似地用以下函数给出:
y=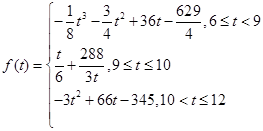
求从上午 点到中午
点到中午 点,通过该收费站用时最多的时刻。
点,通过该收费站用时最多的时刻。