已知椭圆 :
: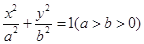 的左焦点为
的左焦点为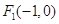 ,且过点
,且过点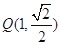 .
.
(1)求椭圆 的方程;
的方程;
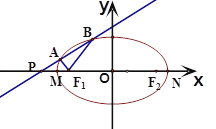
(2)设过点P(-2,0)的直线与椭圆E交于A、B两点,且满足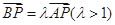 .
.
①若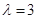 ,求
,求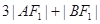 的值;
的值;
②若M、N分别为椭圆E的左、右顶点,证明: 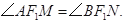
设
的内角
的对边分别为
,
.
(Ⅰ)求
;
(Ⅱ)若
,求
.
等差数列 中, .
(I)求
的通项公式;
(II)设
,求数列
的前
项和
.
已知函数
.
(Ⅰ)若
时,
,求
的最小值;
(Ⅱ)设数列
的通项
,证明:
.
已知双曲线
的左、右焦点分别为
,离心率为3,直线
与
的两个交点间的距离为
.
(Ⅰ)求
;
(Ⅱ)设过
的直线
与
的左、右两支分别交于
两点,且
,证明:
成等比数列.
甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判.设各局中双方获胜的概率均为
,各局比赛的结束相互独立,第1局甲当裁判.
(Ⅰ)求第4局甲当裁判的概率;
(Ⅱ)X表示前4局中乙当裁判的次数,求X的数学期望.