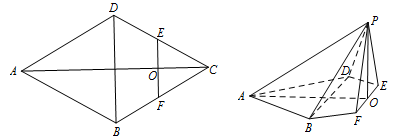
(本小题满分12分)如图,在菱形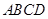 中,
中, ,
,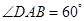 ,
, 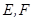 分别是边
分别是边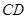 ,
,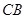 的中点,
的中点,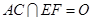 ,沿
,沿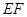 将△
将△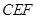 翻折到△
翻折到△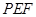 ,连接
,连接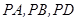 ,得到如图的五棱锥
,得到如图的五棱锥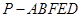 .
.
(Ⅰ)求证: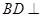 平面
平面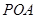 ;
;
(Ⅱ)若 ,求二面角
,求二面角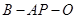 的大小.
的大小.
已知菱形ABCD中,AB=4, 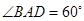 (如图1所示),将菱形ABCD沿对角线
(如图1所示),将菱形ABCD沿对角线 翻折,使点
翻折,使点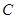 翻折到点
翻折到点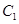 的位置(如图2所示),点E,F,M分别是AB,DC1,BC1的中点.
的位置(如图2所示),点E,F,M分别是AB,DC1,BC1的中点.
(Ⅰ)证明:BD //平面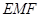 ;
;
(Ⅱ)证明: ;
;
(Ⅲ)当 时,求线段AC1的长.
时,求线段AC1的长.

某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是 ,样本数据分组为
,样本数据分组为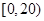 ,
, ,
, ,
, ,
,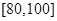 .
.
(Ⅰ)求直方图中 的值;
的值;
(Ⅱ)如果上学所需时间不少于1小时的学生可申请在学校住宿,请估计学校600名新生中有多少名学生可以申请住宿.
已知函数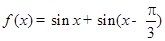 .
.
(Ⅰ)求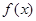 的单调递增区间;
的单调递增区间;
(Ⅱ)在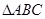 中,角
中,角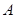 ,
, ,
, 的对边分别为
的对边分别为 .已知
.已知 ,
, ,试判断
,试判断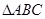 的形状.
的形状.
已知函数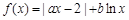 (x>0).
(x>0).
(1)若a=1,f(x)在(0,+∞)上是单调增函数,求b的取值范围;
(2)若a≥2,b=1,求方程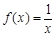 在(0,1]上解的个数.
在(0,1]上解的个数.
已知数列 ,
,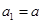 ,且
,且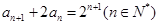 ,
,
(1)若 成等差数列,求实数
成等差数列,求实数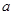 的值;
的值;
(2)数列 能为等比数列吗?若能,试写出它的充要条件并加以证明;若不能,请说明理由。
能为等比数列吗?若能,试写出它的充要条件并加以证明;若不能,请说明理由。