在平面直角坐标xOy中，（如图）正方形OABC的边长为4，边OA在x轴的正半轴上，边OC在y轴的正半轴上，点D是OC的中点，BE⊥DB交x轴于点E.
⑴求经过点D、B、E的抛物线的解析式；
⑵将∠DBE绕点B旋转一定的角度后，边BE交线段OA于点F，边BD交y轴于点G，交⑴中的抛
物线于M（不与点B重合），如果点M的横坐标为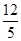
，那么结论OF=
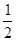DG能成立吗？请说明理由.
⑶过⑵中的点F的直线交射线CB于点P，交⑴中的抛物线在第一象限的部分于点Q，且使△PFE为等腰三角形，求Q点的坐标.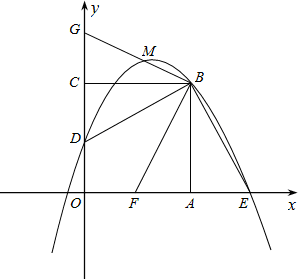
观察下面三行数：
-2， 4， -8， 16， -32， 64，……①
0, 6, -6, 18, -30, 66, ……②
-1, 2, -4, 8, -16, 32, ……③
(1)第①行数的第21个数是（可用幂的形式表示）
第②行数的第21个数是
第③行数的第21个数是
(2)若第①行数的某个数为x，它与第②行数、第③行数中与它相对应的数的和
为-318，求x
某商店出售茶杯、茶壶，茶杯每只定价4元，茶壶每只定价20元，该商店的优惠办法
是买一只茶壶赠一只茶杯，某顾客欲购买茶壶5只，茶杯
只（茶杯数超过5只）。
（1）用含的式子表示这位顾客应付款的钱数；
（2）当
时，应付款多少元？
（1）化简
（2）先化简，再求值：
，其中
，
计算：（1）
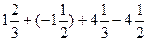（2）
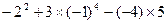
（3） 
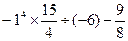（4）用简便方法计算：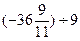
如图所示，在数轴上有三个点，A，B，C，回答下列问题。
（1）A，C两点间的距离是多少？
（2）若E点与B点的距离是8，则E点表示的数是什么？