某学校为了解八年级学生的课外阅读情况，钟老师随机抽查部分学生，并对其暑假期间的课外阅读量进行统计分析，绘制成如图所示，但不完整的统计图．根据图示信息，解答下列问题：
（1）求被抽查学生人数及课外阅读量的众数；
（2）求扇形统计图汇总的a、b值；
（3）将条形统计图补充完整；
（4）若规定：假期阅读3本以上（含3本）课外书籍者为完成假期作业，据此估计该校600名学生中，完成假期作业的有多少人？
已知，如图，以点P（﹣1，0）为圆心的圆，交x轴于A、C两点（A在C的左侧），交y轴于B、D两点（B在D的上方），且∠BAC＝30°，
（1）如图①求⊙P的半径及点B的坐标；
（2）点Q是⊙P上任意一点，求△ABQ面积S的取值范围；
（3）如图②，已知点M（－5，0），过M作直线y=kx+b交y轴于点N，
①若MN//AB，试判断MN与⊙P的位置关系，并说明理由；
②在该直线上存在一点G，使以G、A、C为顶点的三角形是直角三角形，且满足条件的点G有且只有三个不同位置，求直线MN的函数关系式．
已知直线AB与
轴、
轴分别交于点A和点B，AB=10，且tan∠BAO=
，以OA、OB为边作矩形OACB，点F 在BC上，过点F作AB的垂线，交AB于点D，交OA于点E，若⊙P是△AOB的内切圆，切点分别为M、N、G，
（1）求证：四边形PMON是正方形；
（2）求⊙P的半径;
（3）求当FE与⊙P相交的弦长为2．4时点F的坐标．
如图，已知Rt△ABC和Rt△EBC，∠B＝90°，∠E=∠ACB，AD//BC交EC于点D，以边AC上的点O为圆心的⊙O过点D、A，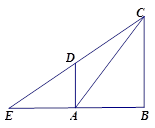
（1）用直尺和圆规确定并标出圆心O；
（2）判断⊙O与EC的位置关系并说明理由．
（1）如图，在Rt△ABC中，∠C=90°，AC=BC，小明为了求tan67．5°值，他延长CB到D，使BD=BA，连接AD，请你根据图形计算tan67．5°；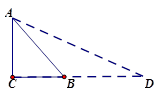
（2）请你仿照小明的方法构造图形求tan75°．
如图，AB是⊙O的直径，CD是⊙O的切线，切点为D，CD与AB的延长线相交于点E，∠ADC＝60°．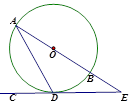
（1）求证：△ADE是等腰三角形；
（2）若AD＝2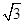
，求BE的长．