如图，正方形ABCD中，E、F分别是边AD、CD上的点，DE=CF，AF与BE相交于O，DG⊥AF，垂足为G。
（1）求证：AF⊥BE；
（2）试探究线段AO、BO、GO的长度之间的数量关系；
（3）若GO：CF=4：5，试确定E点的位置。
如图，在□ABCD中，F是AD的中点，延长BC到点E，使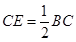
，连接DE，CF．
（1）求证：四边形CEDF是平行四边形；
（2）若AB＝4，AD＝6，∠B＝60°，求DE的长．
如图，在△OAB中，∠OAB＝90°，∠AOB＝30°，OB＝8．以OB为边，在△OAB外作等边△OBC，D是OB的中点，连接AD并延长交OC于E．求证：四边形ABCE是平行四边形．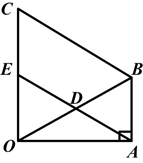
如图，四边形ABCD为等腰梯形，AD∥BC，连接AC、BD，在平面内将△DBC沿BC翻折得到△EBC．
（1）四边形ABEC一定是什么四边形？
（2）证明你在（1）中所得出的结论．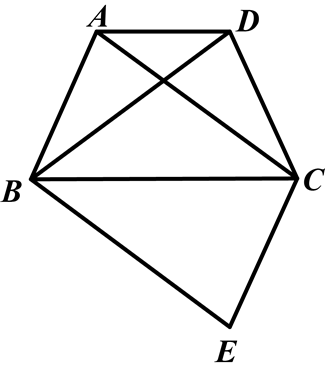
如图，在□ABCD中，M、N分别是AD，BC的中点，连接AN，CM．求证：△ABN≌△CDM．
如图，在Rt△ABC中，∠ACB＝90°，以AC为一边向外作等边三角形ACD，点E为AB的中点，连接DE．
（1）证明：DE∥CB；
（2）探索AC与AB满足怎样的数量关系时，四边形DCBE是平行四边形．