如图,正四棱柱 中,底面边长为2,侧棱长为3,E为BC的中点,F、G分别为
中,底面边长为2,侧棱长为3,E为BC的中点,F、G分别为 、
、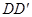 上的点,且CF=2GD=2.求:
上的点,且CF=2GD=2.求:
(1)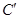 到面EFG的距离;
到面EFG的距离;
(2)DA与面EFG所成的角的正弦值;
(3)在直线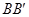 上是否存在点P,使得DP//面EFG?,若存在,找出点P的位置,若不存在,试说明理由。
上是否存在点P,使得DP//面EFG?,若存在,找出点P的位置,若不存在,试说明理由。
已知函数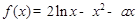 .
.
(Ⅰ)当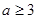 时,讨论函数
时,讨论函数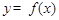 在[
在[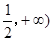 上的单调性;
上的单调性;
(Ⅱ)如果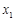 ,
,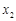
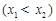 是函数
是函数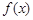 的两个零点,
的两个零点,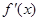 为函数
为函数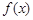 的导数,证明:
的导数,证明: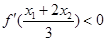 .
.
已知椭圆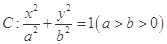 的两个焦点
的两个焦点 和上下两个顶点
和上下两个顶点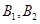 是一个边长为2且∠F1B1F2为
是一个边长为2且∠F1B1F2为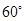 的菱形的四个顶点.
的菱形的四个顶点.
(1)求椭圆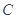 的方程;
的方程;
(2)过右焦点F2 ,斜率为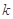 (
(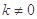 )的直线
)的直线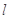 与椭圆
与椭圆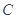 相交于
相交于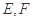 两点,A为椭圆的右顶点,直线
两点,A为椭圆的右顶点,直线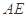 、
、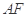 分别交直线
分别交直线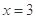 于点
于点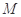 、
、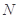 ,线段
,线段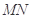 的中点为
的中点为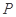 ,记直线
,记直线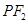 的斜率为
的斜率为 .求证:
.求证: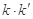 为定值.
为定值.
已知数列 前n项和为
前n项和为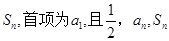 成等差数列.
成等差数列.
(I)求数列 的通项公式;
的通项公式;
(II)数列满足 ,求证:
,求证: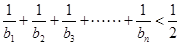 .
.
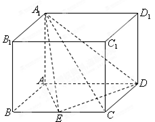
如图,四棱柱 的底面
的底面 是平行四边形,且
是平行四边形,且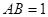 ,
,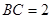 ,
,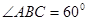 ,
,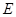 为
为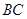 的中点,
的中点,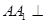 平面
平面 .
.
(Ⅰ)证明:平面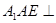 平面
平面 ;
;
(Ⅱ)若 ,试求异面直线
,试求异面直线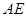 与
与 所成角的余弦值;
所成角的余弦值;
(Ⅲ)在(Ⅱ)的条件下,试求二面角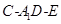 的余弦值.
的余弦值.
在某校教师趣味投篮比赛中,比赛规则是:每场投6个球,至少投进4个球且最后2个球都投进者获奖;否则不获奖.已知教师甲投进每个球的概率都是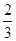 .
.
(Ⅰ)记教师甲在每场的6次投球中投进球的个数为X,求X的分布列及数学期望;
(Ⅱ)求教师甲在一场比赛中获奖的概率.