某车站每天上午发出两班客车(每班客车只有一辆车)。第一班客车在8∶00,8∶20,8∶40这三个时刻随机发出,且在8∶00发出的概率为 ,8∶20发出的概率为
,8∶20发出的概率为 ,8∶40发出的概率为
,8∶40发出的概率为 ;第二班客车在9∶00,9∶20,9∶40这三个时刻随机发出,且在9∶00发出的概率为
;第二班客车在9∶00,9∶20,9∶40这三个时刻随机发出,且在9∶00发出的概率为 ,9∶20发出的概率为
,9∶20发出的概率为 ,9∶40发出的概率为
,9∶40发出的概率为 .两班客车发出时刻是相互独立的,一位旅客预计8∶10到站.求:
.两班客车发出时刻是相互独立的,一位旅客预计8∶10到站.求:
(1)请预测旅客乘到第一班客车的概率;
(2)求旅客候车时间 的分布列和数学期望。
的分布列和数学期望。
如图,在直三棱柱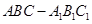 中,
中,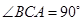 ,
,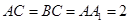 ,
,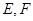 分别是
分别是 的中点。
的中点。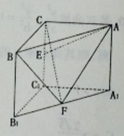
(1)求证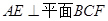 ;
;
(2)求二面角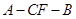 的平面角的余弦值。
的平面角的余弦值。
在 中,角
中,角 的对边分别是
的对边分别是 ,且
,且 。
。
(1)求证 。
。
(2)若 ,
, ,求
,求 的面积。
的面积。
选修4-5:不等式证明
设函数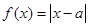
(1)若 的解集为R,求实数a的取值范围;
的解集为R,求实数a的取值范围;
(2)若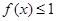 的解集为
的解集为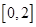 ,且
,且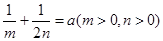 ,求证:
,求证: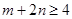 .
.
(本小题满分10分)选修4-4:坐标系与参数方程
已知椭圆C: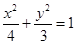 ,直线
,直线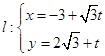 (t为参数).
(t为参数).
(1)写出椭圆C的参数方程及直线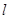 的普通方程;
的普通方程;
(2)设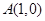 ,若椭圆C上的点P满足到点A的距离与其到直线
,若椭圆C上的点P满足到点A的距离与其到直线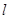 的距离相等,求点P的坐标.
的距离相等,求点P的坐标.
(本小题满分10分)选修4-1:几何证明选讲
如图,AB是圆O的一条切线,切点为B,直线ADE,CFD,CGE,都是圆O的割线,已知AC=AB..
(1)求证: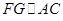 ;
;
(2)若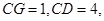 求
求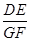 的值.
的值.