如图所示:在平面直角坐标系中,圆M经过原点O且与X轴Y轴分别相交于A(-6,0),B(0,-8)两点
(1)请写出直线 AB的解析式
(2)若有一抛物线的对称轴平行于Y轴且经过点M,顶点C在圆M上,开口向下且经过点B。求此抛物线的函数表达式
(3)设(2)中的抛物线交X轴于D、E两点,在抛物线上是否存在点P,使得  。若存在,请直接写出所有点P的坐标,若不存在,请说明理由
。若存在,请直接写出所有点P的坐标,若不存在,请说明理由
已知关于x的一元二次方程x2-(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若周长为16的等腰△ABC的两边AB,AC的长是方程的两个实数根,求k的值.
如图△ABC中,DE∥BC,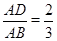 ,M为BC上一点,AM交DE于N.
,M为BC上一点,AM交DE于N.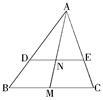
(1)若AE=4,求EC的长;
(2)若M为BC的中点,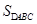 =36,求
=36,求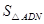
解方程:
(1)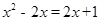 =0
=0
(2)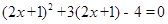 .
.
如图,在平面直角坐标系中,O为坐标原点.△ABC的边BC在x轴上,A、C两点的坐标分别为A(0,m)、C(n,0),B(﹣5,0),且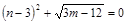 ,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为t秒.
,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为t秒.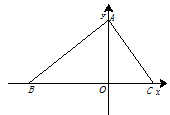
(1)求A、C两点的坐标;
(2)连接PA,用含t的代数式表示△POA的面积;
(3)当P在线段BO上运动时,是否存在一点P,使△PAC是等腰三角形?若存在,请写出满足条件的所有P点的坐标并求t的值;若不存在,请说明理由.
阅读材料:矩形的四个内角都是直角,矩形的对边平行且相等.利用阅读材料解决下列问题:如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD沿CE折叠后,使点D恰好落在对角线AC上的F处.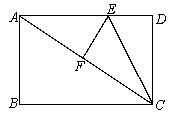
(1)求EF的长;
(2)求梯形ABCE的面积.