如图,梯形ABCD中,AD∥BC,∠BAD=90°,CE⊥AD于点E,AD=4cm,BC=2cm,AB=3cm.从初始时刻开始,动点P、Q分别从点A、B同时出发,运动速度均为1 cm/s,动点P沿A→B→C→E的方向运动,到点E停止;动点Q沿B→C→E→D的方向运动,到点D停止.设运动时间为 s,
s,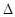 PAQ的面积为y cm2.(这里规定:线段是面积为0的三角形)解答下列问题:
PAQ的面积为y cm2.(这里规定:线段是面积为0的三角形)解答下列问题: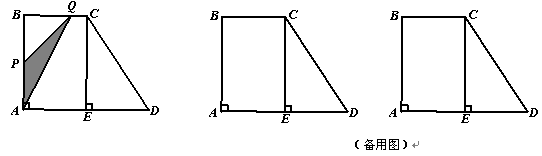
(1)当x=" 2" s时,y=________cm2;当 =
=  s时,y=________cm2;
s时,y=________cm2;
(2)当动点P在线段BC上运动,即3 ≤ x ≤ 5时,求y与 之间的函数关系式,并求出
之间的函数关系式,并求出 时
时 的值;
的值;
(3)当动点P在线段CE上运动,即5 < x ≤ 8 时,求y与 之间的函数关系式;
之间的函数关系式;
(4)直接写出在整个运动过程中,使PQ与四边形ABCE的对角线平行的所有x的值.
如图1,A1B1和A2B2是水面上相邻的两条赛道(看成两条互相平行的线段).甲是一名游泳运动健将,乙是一名游泳爱好者,甲在赛道A1B1上从A1处出发,到达B1后,以同样的速度返回A1处,然后重复上述过程;乙在赛道A2B2上以2m/s的速度从B2处出发,到达A2后以相同的速度回到B2处,然后重复上述过程(不考虑每次折返时的减速和转向时间).若甲、乙两人同时出发,设离开池边B1B2的距离为y(m),运动时间为t(s),甲游动时,y(m)与t(s)的函数图象如图2所示.
(1)赛道的长度是m,甲的速度是m/s;
(2)分别写出甲在 和
和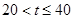 时,y关于t的函数关系式:
时,y关于t的函数关系式:
当 ,y=;当
,y=;当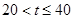 时,y=;
时,y=;
(3)在图2中画出乙在2分钟内的函数大致图象(用虚线画);
(4)请你根据(3)中所画的图象直接判断,若从甲、乙两人同时开始出发到2分钟为止,甲、乙共相遇了几次?2分钟时,乙距池边B1B2的距离为多少米。
已知:二次函数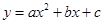
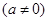 中的
中的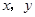 满足下表:
满足下表:
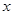 |
…… |
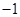 |
0 |
1 |
2 |
3 |
…… |
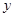 |
…… |
0 |
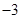 |
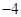 |
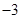 |
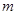 |
…… |
(1)求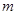 的值;
的值;
(2)根据上表求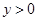 时的
时的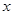 的取值范围;
的取值范围;
(3)若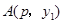 ,
,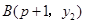 两点都在该函数图象上,且
两点都在该函数图象上,且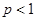 ,试比较
,试比较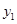 与
与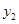 的大小.
的大小.
某学校体育场看台的侧面如图阴影部分所示,看台有四级高度相等的小台阶,每级小台阶都为0.4米.现要做一个不锈钢的扶手AB及两根与FG垂直且长均为l米的不锈钢架杆AD和BC(杆子的底端分别为D,C),且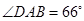 .
.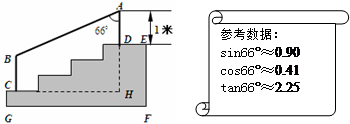
(1)求点D与点C的高度差DH的长度;
(2)求所用不锈钢材料的总长度.(结果精确到0.1米)
对某校九 年级随机抽取若干名学生进行体能测试,成绩按A、B、C、D四个等级进行了评定.现将抽取学生的成绩评定结果进行分析,并绘制扇形统计图和条形统计图如下: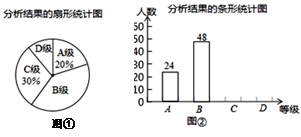
根据上述信息完成下列问题:
(1)这次抽取的样本的容量为;图①中“D级”对应的扇形圆心角度数为°
(2)请在图②中把条形统计图补充完整;
(3)已知该校九年级共有学生750名,请你估计体能达到A级和B级的共约有多少人.
盒子中有4个球,每个球上写有1~4中的一个数字,不同的球上数字不同.
(1)若从盒中取三个球,以球上所标数字为线段的长,则能构成三角形的概率是多少?
(2)若小明从盒中取出一个球,放回后再取出一个球,然后让小华猜两球上的数字之和,你认为小华猜和为多少时 ,猜中的可能性大.请说明理由.