如图所示,已知在直角梯形 中,
中,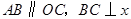 轴于点
轴于点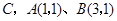 .动点
.动点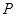 从
从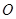 点出发,沿
点出发,沿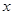 轴正方向以每秒1个单位长度的速度移动.过
轴正方向以每秒1个单位长度的速度移动.过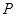 点作
点作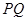 垂直于直线
垂直于直线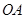 ,垂足为
,垂足为 .设
.设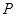 点移动的时间为
点移动的时间为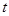 秒(
秒(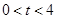 ),
), 与直角梯形
与直角梯形 重叠部分的面积为
重叠部分的面积为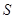 .
.
(1)求经过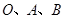 三点的抛物线解析式;
三点的抛物线解析式;
(2)求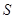 与
与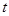 的函数关系式;
的函数关系式;
(3)将 绕着点
绕着点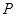 顺时针旋转
顺时针旋转 ,是否存在
,是否存在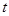 ,使得
,使得 的顶点
的顶点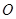 或
或 在抛物线上?若存在,直接写出
在抛物线上?若存在,直接写出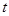 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
计算:
(1)已知:(x+2)2=25,求x;
(2)计算:
有一进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分的进水量和出水量有两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.
(1)当4≤x≤12时,求y关于x的函数解析式;
(2)直接写出每分进水,出水各多少升.
如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线l,过点B作一直线(在山的旁边经过),与 相交于D点,经测量∠ABD=135°,BD=800米,求直线
相交于D点,经测量∠ABD=135°,BD=800米,求直线 上距离D点多远的C处开挖?(
上距离D点多远的C处开挖?( ≈1.414,精确到1米)
≈1.414,精确到1米)
已知:如图,点 在同一直线上,
在同一直线上, ,
, ,
, ∥
∥ .求证:
.求证: .
.
如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动。它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负。如果从A到B记为:A→B(+1,+3);从C到D记为:C→D(+1,-2)。其中第一个数表示左右方向,第二个数表示上下方向,那么图中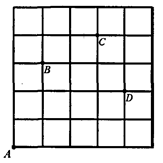
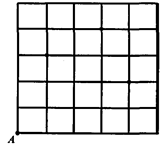
(1)A→C( , ),C→(-2, );
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(3)假如这只甲虫从A处去甲虫P处的行走路线依次为
(+2,+2),(+1,-1),(-2,+3),请在图中标出P的位置.