如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE。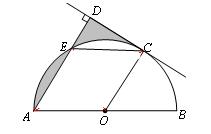
(1)判断CD与⊙O的位置关系,并证明你的结论;
(2)若E是AC弧 的中点,⊙O的半径为1,求图中阴影部分的面积。
(本题10分)在平面直角坐标系xOy中, A、B两点分别在x轴、y轴的正半轴上,且OB = OA=3.
(1)求点A、B的坐标;(2)已知点C(-2,2),求△BOC的面积; (3)点P是第一象限角平分线上一点,若 ,求点P的坐标.
,求点P的坐标.
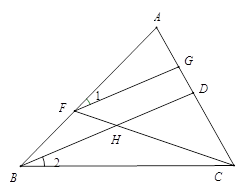
(本题6分)如图:BD平分∠ABC,F在AB上,G在AC上,FC与BD相交于点H.∠GFH+∠BHC=180°,求证: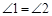 .
.
(本题6分)已知如图:AD∥BC,E、F分别在DC、AB延长线上.∠DCB=∠DAB,AE⊥EF,∠DEA=30°.
(1)求证:DC//AB.
(2)求∠AFE的大小.
(本题6分)已知直线AB和CD相交于点O,∠AOC为锐角,过O点作直线OE、OF.若OE⊥CD,OF平分∠AOE,求∠AOF+∠COF的度数.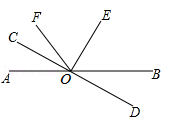
(本题6分)
(1)制作一个表面积为12平方分米的正方体纸盒,棱长应为多少分米?
(2)如果2a-1的平方根是±3,3a+2b+4的立方根是3,求a+b的平方根.