(本题10分)在平面直角坐标系xOy中, A、B两点分别在x轴、y轴的正半轴上,且OB = OA=3.
(1)求点A、B的坐标;(2)已知点C(-2,2),求△BOC的面积; (3)点P是第一象限角平分线上一点,若 ,求点P的坐标.
,求点P的坐标.
今年6月份,我市某果农收获荔枝30吨,香蕉13吨.现计划租用甲、乙两种货车共10辆将这批水果全部运往深圳,已知甲种货车可将荔枝4吨和香蕉1吨,乙种货车可将荔枝和香蕉各2吨.
(1)该果农安排甲、乙两种货车时有几种方案?请你帮 助设计出来?
助设计出来?
(2)若甲种货车每辆要付运输费2000元,乙种货车每辆要付运输1300元,则该果农应选择哪能种方案才能使运输费最少?最少动费是多少?
. 七年级(2)班有50名学生,老师安排每人制作一 件A型或B型的陶艺品,学校现有甲种制作材料36kg,乙种制作材料29kg,制作A、B两种型号的陶艺品用料情况如下表:
件A型或B型的陶艺品,学校现有甲种制作材料36kg,乙种制作材料29kg,制作A、B两种型号的陶艺品用料情况如下表:
| 需甲种材料 |
需乙种材料 |
|
| 1件A型陶艺品 |
0.9kg |
0.3kg |
| 1件B型陶艺品 |
0.4kg |
1kg |
(1)设制作B型陶艺品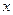 件,
件, 求
求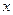 的取值范围.
的取值范围.
(2)请你根据学校现有材料,分别写出七年级(2)班制作A型和B型陶艺品的件数.
为了保护环境,某企业决定购买10台污水处理设备,现有A.B两种型号的设备,其中每台的价格.月处理污水量及年消耗费如下表:
| A型 |
B型 |
|
| 价格(万元/台) |
12 |
10 |
| 处理污水量(吨/月) |
240 |
200 |
| 年消耗费(万元/台) |
1 |
1 |
经预算,该企业购买设备的资金不高于105万元。
(1)请你设计该企业有几种购买方案;
(2)若企业每月产生的污水量为2040吨,为了节约资金,应选择哪种购买方案;
(3)在第(2)问的条件下,若每台设备的使用年限10年,污水厂处理污水费为每吨10元,请你计算,该企业自己处理污水与将污水排到污 水厂处理相比较,10年节约资金多少万元?(注:企业处理污水的费用包括购买设备的资金和消耗费)
水厂处理相比较,10年节约资金多少万元?(注:企业处理污水的费用包括购买设备的资金和消耗费)
解不等式组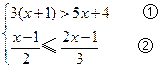 ,并将解集在数轴上表示出来.
,并将解集在数轴上表示出来. 22.
22.
解不等式组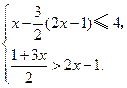 把解集表示在数轴上,并求
把解集表示在数轴上,并求 出不等式组的整数
出不等式组的整数