今年6月份，我市某果农收获荔枝30吨，香蕉13吨．现计划租用甲、乙两种货车共10辆将这批水果全部运往深圳，已知甲种货车可将荔枝4吨和香蕉1吨，乙种货车可将荔枝和香蕉各2吨．
（1）该果农安排甲、乙两种货车时有几种方案？请你帮
助设计出来？
（2）若甲种货车每辆要付运输费2000元，乙种货车每辆要付运输1300元，则该果农应选择哪能种方案才能使运输费最少？最少动费是多少？
如图，用三种大小不同的五个正方形和一个缺角的长方形拼成长方形ABCD，其中，NH=NG=1cm，设BF=acm．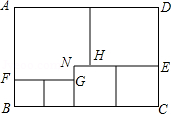
（1）用含a的代数式表示CE= cm，DE= cm；
（2）求长方形ABCD的周长．（用含a的代数式表示）
把下列各数填在相应的大括号内：
，0，3.14，﹣
，﹣0.55，8，﹣2．
正数集合：{ …}；
整数集合：{…}；
分数集合：{ …}．
计算：（2a2﹣4+3a）﹣2（a+a2﹣
）
如图，直线l：y=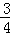
x+6交x、y轴分别为A、B两点，C点与A点关于y轴对称．动点P、Q分别在线段AC、AB上（点P不与点A、C重合），满足∠BPQ=∠BAO．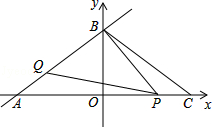
（1）点A坐标是 ，点B的坐标 ，BC= ．
（2）当点P在什么位置时，△APQ≌△CBP，说明理由．
（3）当△PQB为等腰三角形时，求点P的坐标．
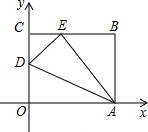
如图，OABC是一张放在平面直角坐标系中的长方形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=10，OC=8，在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，求D、E两点的坐标．