问题提出：
（1）如图1，已知，试确定一点，使得以，，，为顶点的四边形为平行四边形，请画出这个平行四边形；
问题探究：
（2）如图2，在矩形中，，，若要在该矩形中作出一个面积最大的，且使，求满足条件的点到点的距离；
问题解决：
（3）如图3，有一座塔，按规定，要以塔为对称中心，建一个面积尽可能大的形状为平行四边形的景区．根据实际情况，要求顶点是定点，点到塔的距离为50米，，那么，是否可以建一个满足要求的面积最大的平行四边形景区？若可以，求出满足要求的平行四边形的最大面积；若不可以，请说明理由．（塔的占地面积忽略不计）
如图①，在Rt△ABC中，∠BAC＝90°，AB＝AC＝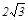
，D、E两点分别在AC、BC上，且DE∥AB，CD＝
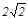．将△CDE绕点C顺时针旋转，得到△CD’E’(如图②，点D’、E’分别与点D、E对应)，点E’在AB上，D’E’与AC相交于点M．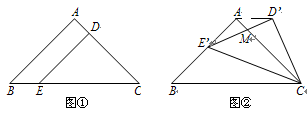
(1)求∠ACE’的度数；
(2)求证：四边形ABCD’是梯形；
(3)求△AD’M的面积．
某商场将每台进价为3000元的彩电以3900元的销售价售出，每天可销售出6台．假设这种品牌的彩电每台降价100x(x为正整数)元，每天可多售出3x台．(注：利润＝销售价－进价)
(1)设商场每天销售这种彩电获得的利润为y元，试写出y与x之间的函数关系式；
(2)销售该品牌彩电每天获得的最大利润是多少？此时，每台彩电的销售价是多少时，彩电的销售量和营业额均较高？
某市图书馆的自然科学、文学艺术、生活百科和金融经济四类图书比较受读者的欢迎．为了更好地为读者服务，该市图书馆决定近期添置这四方面的图书，为此图书管理员对2007年5月份四类图书的借阅情况进行了统计，得到了四类图书借阅情况的频数表．
| 图书种类 |
自然科学 |
文学艺术 |
生活百科 |
金融经济 |
| 频数(借阅人数) |
2000 |
2400 |
1600 |
2000 |
请你根据表中提供的信息，解答以下问题：
(1)填空：表中数据的极差是______________；
(2)请在下边的圆中用扇形统计图表示四类图书的借阅情况；
(3)如果该市图书馆要添置这四类图书10000册，请你估算“文学艺术”类图书应添置多少册较合适？
如图，四边形ABCD内接于⊙O，BD是⊙O的直径，AE⊥CD，垂足为E，DA平分∠BDE．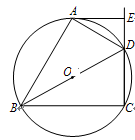
(1)求证：AE是⊙O的切线；
(2)若∠DBC＝30°，DE＝1cm，求BD的长．
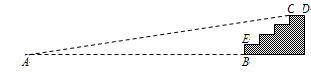
某商场门前的台阶截面如图所示．已知每级台阶的宽度(如CD)均为30cm，高度(如BE)均为20cm．为了方便残疾人行走，商场决定将其中一个门的门前台阶改造成供轮椅行走的斜坡，并且设计斜坡的倾斜角为9°．请计算从斜坡起点A到台阶前的点B的水平距离．(参考数据：sin9°≈0.16，cos9°≈0.99，tan9°≈0.16)