如图1,在第一象限内,直线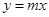 与过点
与过点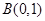 且平行于
且平行于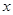 轴的直线
轴的直线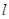 相交于点
相交于点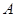 ,半径为
,半径为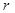 的⊙
的⊙ 与直线
与直线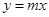 、
、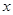 轴分别相切于点
轴分别相切于点 、
、 ,且与直线
,且与直线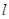 分别交于不同的
分别交于不同的 、
、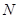 两点.
两点.
(1)当点A的坐标为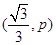 时,
时,
① 填空: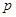 = ,
= ,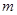 = ,
= ,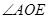 = ;
= ;
②如图2,连结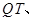
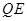 ,
,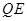 交直线
交直线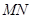 于
于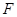 ,当
,当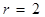 时,试说明以
时,试说明以 、
、  、
、 、
、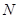 为顶点的四边形是等腰梯形;
为顶点的四边形是等腰梯形;
(2)在图1中,连结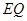 并延长交⊙
并延长交⊙ 于点
于点 ,试探索:对不同的
,试探索:对不同的 取值,经过
取值,经过 、
、 、
、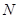 三点的抛物线
三点的抛物线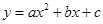 ,
,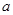 的值会变化吗?若不变,求出
的值会变化吗?若不变,求出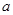 的值;若变化,请说明理由.
的值;若变化,请说明理由.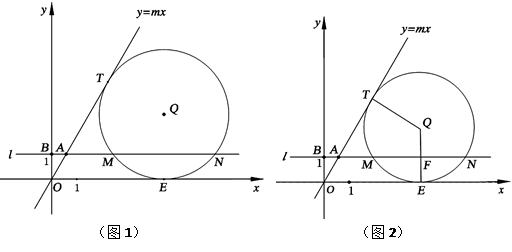
下列由四舍五入得到的近似数精确到哪一位?各有几个有效数字?
①230;②18.3;③0.0098;④3.4万;⑤20.010.
治理沙漠的植树活动中,某县今年派出的青年志愿者为100人,每人完成植树任务50棵,计划明年派出人数增加p%,每人植树任务增加q%
(1)写出明年计划的总植树的代数式;
(2)并求出当p=10,q=20时的植树总数.
(1)分别求出代数式 和
和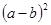 值其中(1)
值其中(1) (2)a=5,b=3(3)观察(1)中的(1)(2)你发现了什么?
(2)a=5,b=3(3)观察(1)中的(1)(2)你发现了什么?
找规律(用n表示第n个数)
(1)1,4,9,16,25,…,请写出第n个数,
(2)2,5,10,17,26,…,请写出第n个数,
(3)3,6,9,12,15,18,…,请写出第n个数,
(4)2,4,8,16,32,64,…,请写出第n个数,
一台电视机成本价为a元,销售价比成本价增长25%,因库存积压,所以就接销售价的70%出售,问每台电视机的实际售价是多少元?