(本小题满分12分)在国家法定工作日内,每周满工作量的时间为40小时,若每周工作时间不超过40小时,则每小时工资25元;如因需要加班,超过40小时的每小时工资为50元.某公务员在一周内工作时间为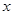 小时,但他须交纳个人住房公积金和失业保险(这两项费用为每周总收入的10%).试分析算法步骤并画出其每周净得工资
小时,但他须交纳个人住房公积金和失业保险(这两项费用为每周总收入的10%).试分析算法步骤并画出其每周净得工资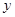 元的算法的程序框图.(注:满工作量外的工作时间为加班)
元的算法的程序框图.(注:满工作量外的工作时间为加班)
数列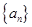 是首项
是首项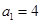 的等比数列,且
的等比数列,且 ,
,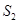 ,
,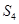 成等差数列.
成等差数列.
(Ⅰ)求数列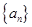 的通项公式;
的通项公式;
(Ⅱ)若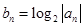 ,设
,设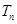 为数列
为数列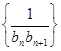 的前
的前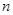 项和,若
项和,若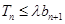 对一切
对一切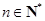 恒
恒
成立,求实数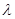 的最小值.
的最小值.
在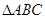 中,
中,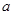 、
、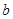 、
、 分别是角
分别是角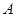 、
、 、
、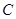 的对边,
的对边,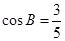 ,且符合
,且符合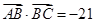 .
.
(Ⅰ)求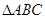 的面积;
的面积;
(Ⅱ)若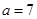 ,求角
,求角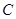 .
.
已知二次函数 和“伪二次函数”
和“伪二次函数” 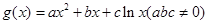 .
.
(Ⅰ)证明:只要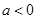 ,无论
,无论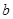 取何值,函数
取何值,函数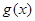 在定义域内不可能总为增函数;
在定义域内不可能总为增函数;
(Ⅱ)在同一函数图像上任意取不同两点A(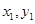 ),B(
),B(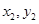 ),线段AB中点为C(
),线段AB中点为C(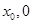 ),记直线AB的斜率为k.
),记直线AB的斜率为k.
(1)对于二次函数 ,求证
,求证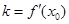 ;
;
(2)对于“伪二次函数” 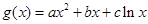 ,是否有(1)同样的性质?证明你的结论。
,是否有(1)同样的性质?证明你的结论。
如图,已知F1、F2分别为椭圆C1: 的上、下焦点,其中F1也是抛物线C2:
的上、下焦点,其中F1也是抛物线C2: 的焦点,点A是曲线C1,C2在第二象限的交点,且
的焦点,点A是曲线C1,C2在第二象限的交点,且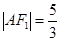

(Ⅰ)求椭圆 1的方程;
1的方程;
(Ⅱ)已知P是椭圆C1上的动点,MN是圆C: 的直径,求
的直径,求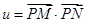 的最大值和最小值.
的最大值和最小值.
目前,在我国部分省市出现了人感染H7N9禽流感病毒,为有效防控,2013年4月下旬,北京疫苗研制工作进入动物免疫原性试验阶段。假定现已研制出批号分别为1,2,3,4,5的五批疫苗,准备在A、B、C三种动物身上做试验,给每种动物做实验所选用的疫苗是从这五个批号中任选其中一个批号的疫苗.
(Ⅰ)求给三种动物注射疫苗的批号互不相同的概率;
(Ⅱ)记给A、B、C三种动物注射疫苗的批号最大数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.