某压力锅结构如图所示。盖好密封锅盖,将压力阀套在出气孔上,给压力锅加热,当锅内气体压强达到一定值时,气体就把压力阀顶起。假定在压力阀被顶起时,停止加热。
(1)若此时锅内气体的体积为V,摩尔体积为V0,阿伏加德罗常数为NA,写出锅内气体分子数的估算表达式。
(2)假定在一次放气过程中,锅内气体对压力阀及外界做功1J,并向外界释放了2J的热量。锅内原有气体的内能如何变化?变化了多少?
(3)已知大气压强P随海拔高度H的变化满足P=P0(1-αH),其中常数α>0。结合气体定律定性分析在不同的海拔高度使用压力锅,当压力阀被顶起时锅内气体的温度有何不同。
如图所示,一小型发电站通过升压变压器B1和降压变压器B2把电能输送给用户(B1和B2都是理想变压器),已知发电机的输出功率为500kW,输出电压为500V,升压变压器B1原、副线圈的匝数比为1∶10,两变压器间输电导线的总电阻为2Ω。降压变压器B2的输出电压为220V。求: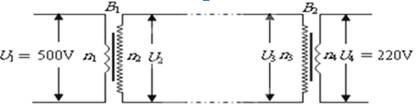
(1)输电导线上损失的功率;
(2)降压变压器B2的原、副线圈的匝数比。
弹簧振子以O点为平衡位置在B、C两点之间做简谐运动,B、C相距20cm..t=0时刻振子处于B点,经过0.5s,振子首次到达C点,求:
(1) 振子在5s内通过的路程及5秒末位移大小
(2)振子在B点的加速度大小跟它距O点4cm处P点的加速度大小的比值
如图18所示,光滑的平行金属导轨水平放置,电阻不计,导轨间距为l,左侧接一阻值为R的电阻.区域cdef内存在垂直轨道平面向下的有界匀强磁场,磁场宽度为x.一质量为m、电阻为r的金属棒MN置于轨道上,与导轨垂直且接触良好,受到水平拉力F=(0.5v+0.4) N(v为某时刻金属棒运动的瞬时速度)的作用,从磁场的左边界由静止开始运动.已知l=1 m,m=1 kg,R=0.3 Ω,r=0.2 Ω,x=0.8 m,如果测得电阻R两端的电压U随着时间是均匀增大的,那么: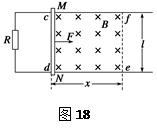
(1)分析并说明该金属棒在磁场中做何种运动;
(2)金属棒到达ef处的速度应该有多大;
(3)分析并求解磁感应强度B的大小.
如图17所示,交流发电机电动势的有效值E=30 V,内阻不计,它通过一个R=6 Ω的指示灯连接降压变压器.变压器输出端并联96只彩色小灯泡,每只灯泡都是“6 V,0.25 W”,灯泡都正常发光,导线电阻不计.求: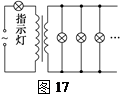
(1)指示灯上的电压;
(2)发电机的输出功率.
一矩形线圈,在匀强磁场中绕垂直磁感线的对称轴转动,形成如图16所示的交变电动势图象,试根据图象求出:
(1)线圈转动的角速度;
(2)电动势的有效值;
(3)t = 1.0×10−2s时,线圈平面和磁场方向的夹角。