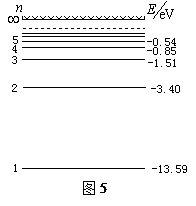
如图5所示为氢原子能级示意图,现有每个电子的动能都是Ee=12.89eV的电子束与处在基态的氢原子束射入同一区域,使电子与氢原子发生正碰。已知碰撞前一个电子和一个氢原子的总动量恰好为零。碰撞后氢原子受激发,跃迁到n=4的能级。求碰撞后电子和受激氢原子的总动能。已知电子的质量me与氢原子的质量mH之比为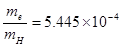 。
。
如图所示,离子源A产生的初速度为零、带电量均为q,质量不同的正离子,被电压为U0的加速电场加速后匀速通过准直管,垂直射入平行板间的匀强偏转电场,偏转后通过极板HM上的小孔S离开电场,经过一段匀速直线运动,垂直于边界MN进入磁感应强度为B的匀强磁场,已知∠MNQ=90°,HO=d,HS=2d.(忽略粒子所受重力)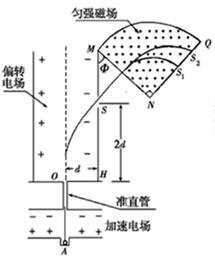
(1)求偏转电场场强E0的大小以及HM与MN的夹角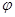
(2)求质量为m的正离子在磁场中做圆周运动的半径;
(3)若质量为9m的正离子恰好垂直打在NQ的中点S1处,试求能打在边界NQ上的正离子的质量范围.
如图所示,两足够长的平行光滑的金属导轨MN、PQ相距为L,导轨平面与水平面的夹角 ,导轨电阻不计,整个装置处于垂直于导轨平面向上的匀强磁场中。长为L的金属棒垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量m、电阻为R。两金属导轨的上端连接一个电阻,其阻值也为R。现闭合开关K ,给金属棒施加一个方向垂直于杆且平行于导轨平面向上的、大小为F=2mg的恒力,使金属棒由静止开始运动,若金属棒上滑距离为s时速度恰达到最大,最大速度vm。(重力加速度为g, sin37°=0.6,cos37°=0.8)求:
,导轨电阻不计,整个装置处于垂直于导轨平面向上的匀强磁场中。长为L的金属棒垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量m、电阻为R。两金属导轨的上端连接一个电阻,其阻值也为R。现闭合开关K ,给金属棒施加一个方向垂直于杆且平行于导轨平面向上的、大小为F=2mg的恒力,使金属棒由静止开始运动,若金属棒上滑距离为s时速度恰达到最大,最大速度vm。(重力加速度为g, sin37°=0.6,cos37°=0.8)求: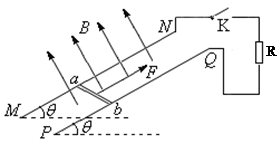
(1)求金属棒刚开始运动时加速度大小;
(2)求匀强磁场的磁感应强度的大小;
(3)求金属棒由静止开始上滑2s的过程中,金属棒上产生的电热Q1
光滑水平地面上,人与滑板A一起以v0=0.5m/s的速度前进,正前方不远处有一横杆,横杆另一侧有一静止滑板B,当人与A行至横杆前,人相对滑板竖直向上起跳(起跳瞬间人与A的水平速度都不发生改变)越过横杆,A从横杆下方通过并与B发生弹性碰撞,之后人刚好落到B上,不计空气阻力,求最终人与B共同速度是多少?已知m人=40kg,mA=5kg,mB=10kg.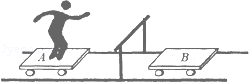
半径为R的玻璃半圆柱体,横截面如图所示,圆心为O,两条平行单色红光沿截面射向圆柱面,方向与底面垂直,光线1的入射点A为圆柱面的顶点,光线2的入射点为B,∠AOB=60°,已知该玻璃对红光的折射率n=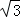 .求两条光线经柱面和底面折射后的交点与O点的距离d;
.求两条光线经柱面和底面折射后的交点与O点的距离d;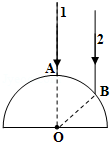
如图所示,左侧装置内存在着匀强磁场和方向竖直向下的匀强电场,装置上下两极板间电势差为U,间距为L,右侧为“梯形”匀强磁场区域ACDH,其中,AH//CD, 。一束电荷量大小为q、质量不等的带电粒子(不计重力、可视为质点),从狭缝S1射入左侧装置中恰能沿水平直线运动并从狭缝S2射出,接着粒子垂直于AH、由AH的中点M射入“梯形”区域,最后全部从边界AC射出。若两个区域的磁场方向均水平(垂直于纸面向里)、磁感应强度大小均为B,“梯形”宽度
。一束电荷量大小为q、质量不等的带电粒子(不计重力、可视为质点),从狭缝S1射入左侧装置中恰能沿水平直线运动并从狭缝S2射出,接着粒子垂直于AH、由AH的中点M射入“梯形”区域,最后全部从边界AC射出。若两个区域的磁场方向均水平(垂直于纸面向里)、磁感应强度大小均为B,“梯形”宽度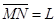 ,忽略电场、磁场的边缘效应及粒子间的相互作用。
,忽略电场、磁场的边缘效应及粒子间的相互作用。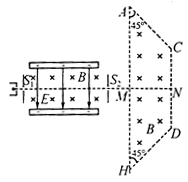
(1)判定这束粒子所带电荷的种类,并求出粒子速度的大小;
(2)求出这束粒子可能的质量最小值和最大值;
(3)求出(2)问中偏转角度最大的粒子在“梯形”区域中运动的时间。