如图所示，左侧装置内存在着匀强磁场和方向竖直向下的匀强电场，装置上下两极板间电势差为U，间距为L，右侧为“梯形”匀强磁场区域ACDH，其中，AH//CD，
。一束电荷量大小为q、质量不等的带电粒子（不计重力、可视为质点），从狭缝S1射入左侧装置中恰能沿水平直线运动并从狭缝S2射出，接着粒子垂直于AH、由AH的中点M射入“梯形”区域，最后全部从边界AC射出。若两个区域的磁场方向均水平（垂直于纸面向里）、磁感应强度大小均为B，“梯形”宽度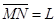
,忽略电场、磁场的边缘效应及粒子间的相互作用。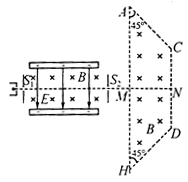
（1）判定这束粒子所带电荷的种类，并求出粒子速度的大小；
（2）求出这束粒子可能的质量最小值和最大值；
（3）求出（2）问中偏转角度最大的粒子在“梯形”区域中运动的时间。
在竖直平面内有一个光滑的半圆轨道，轨道两端连线即直径在竖直方向，轨道半径为0.9m，一个质量为0.5kg的小球以一定的初速度滚上轨道(取g=10m/s2)。求：
（1）小球在最高点不脱离轨道的最小速率是多少？
（2）小球在最高点速率v=4m/s时，小球对轨道的压力是多少？
如图所示，一个质量m＝2kg的物体，受到水平拉力F＝20N由静止开始向右运动，物体与地面间的动摩擦因数为μ=0.5。（取 g＝10m/s2）
求:（1）拉力F在2s内对物体所做的功；
（2）在2s内拉力对物体做功的平均功率．
P、Q是一列简谐横波中的两点，相距9 m，它们各自的振动图线如图所示，那么这列波的波长为多少？波速是多少？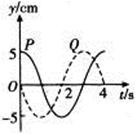
一位学生用如图所示的方法来测定水的折射率，该学生在一个游泳池测得池中水深h="1.2" m（池底水平），用一根竹竿竖直立于池底，浸入水中部分刚好是全长的一半，太阳光与水平方向成θ=37°角射入游泳池，池底竹竿顶端的影子到竹竿底端的距离为L="2.5" m，求水的折射率和光在水中的传播速度。（sin37°=0.6，cos37°=0.8）
如图所示，一平直的传送带以速度v=2m/s匀速运动，传送带把A处的工件运送到B处，A、B相距L=10m．从A处把工件无初速地放到传送带上，经过时间t=6s能传送到B处．求：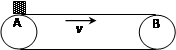
（1）工件在传送带上做匀加速运动的时间
（2）欲使工件用最短时间由A至B，传送带的速度至少为多少？
（3）求出工件从A至B的时间t随皮带运动速度v的变化的函数关系式，并尽可能准确地画出t--v图像，要标明关键坐标值。