在竖直平面内有一个光滑的半圆轨道，轨道两端连线即直径在竖直方向，轨道半径为0.9m，一个质量为0.5kg的小球以一定的初速度滚上轨道(取g=10m/s2)。求：
（1）小球在最高点不脱离轨道的最小速率是多少？
（2）小球在最高点速率v=4m/s时，小球对轨道的压力是多少？
一颗质量m＝10 g的子弹，以速度v＝600 m/s从枪口飞出，子弹飞出枪口时的动能为多少？若测得枪膛长s＝0.6 m，则火药引爆后产生的高温高压气体在枪膛内对子弹的平均推力为多大？
在离地面高为h处竖直上抛一质量为m的物块，抛出时的速度为v0，当它落到地面时速度为v.用g表示重力加速度，则在此过程中物块克服空气阻力所做的功等于( )
A．mgh－ mv2－m |
| B．－mv2－m－mgh |
| C．mgh＋m－mv2 |
| D．mgh＋mv2－m |
如图所示，细绳一端系着质量M＝0.6 kg的物体，静止于水平面上，另一端通过光滑小孔吊着质量m＝0.3 kg的物体，M的中点与圆孔距离为0.2 m，并知M和水平面的最大静摩擦力为2 N．现使此平面绕中心轴线转动，问角速度ω在什么范围m会处于静止状态？(g取10 m/s2)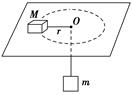
宇宙飞船绕地球做匀速圆周运动时处于完全失重状态，所以在这种环境中已无法用天平称量物体的质量．假设某同学根据这种环境设计了如图所示的装置(图中O为光滑的小孔)来间接测量小物块的质量：给待测小物块一个初速度，使它在桌面上做匀速圆周运动．设航天器中有基本测量工具．
(1)小物块与桌面间的摩擦力可以忽略不计，原因是什么？
(2)实验时需要测量的物理量是什么？
(3)请写出待测小物块质量的表达式．
如图所示，高速公路转弯处弯道圆半径R＝100 m，汽车轮胎与路面间的动摩擦因数μ＝0.23.若路面是水平的，问(1)汽车转弯时不发生径向滑动(离心现象)的最大速率vm为多大？(2)当超过vm时，将会出现什么现象？