为了抓住梵净山文化艺术节的商机，某商店决定购进A、B两种艺术节纪念品．若购进A种纪念品8件，B种纪念品3件，需要950元；若购进A种纪念品5件，B种纪念品6件，需要800元．
（1）求购进A、B两种纪念品每件各需多少元？
（2）若该商店决定购进这两种纪念品共100件，考虑市场需求和资金周转，用于购买这100件纪念品的资金不少于7500元，但不超过7650元，那么该商店共有几种进货方案？
（3）若销售每件A种纪念品可获利润20元，每件B种纪念品可获利润30元，在第（2）问的各种进货方案中，哪一种方案获利最大？最大利润是多少元？
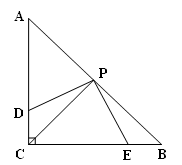
如图，在Rt△ABC中，
∠C=90°，AC=BC，点P是斜边中点，将一个等腰直角三角板绕点P旋转，三角板的两条直角边与AC、BC交于点D、E，连结PC．（1）求证：PC平分∠ACB ；
（2）图中有个等腰直角三角形，分别是；
（3）求证：PD=PE．
如图，点E是正方形ABCD的边DC上一点，把△ADE顺时针旋转△ABF的位置．（1）旋转中心是点 ，旋转角度是
度；（2）若连结EF，则△AEF是 三角形；
（3）若四边形AECF的面积为25，DE=2，求AE的长．
如图，已知：AD为△ABC中BC边的中线，CE∥AB交AD的延长线与点E，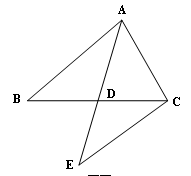
（1）求证：AB=CE；
（2）试判断2AD与(AB+AC) 的大小关系，即2AD
(AB+AC)．（只填“=”、“>”或“<”）
如图，在△ABC中，D是BC边的中点，且AD平分∠BAC，DE⊥AB，DF⊥AC，垂足分别是E，F，求证：△ABC是等腰三角形 ．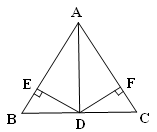
尺规作图：如图，已知点A、点B以及直线l，在直线l上求做一点P，使PA=PB（不写作法，要保留作图痕迹）