如图,P—ABCD是正四棱锥, 是正方体,其中
是正方体,其中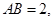
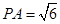
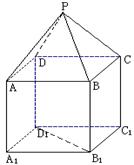
(1)求证: ;
;
(2)求平面PAD与平面 所成的锐二面角
所成的锐二面角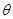 的余弦值;
的余弦值;
(3)求 到平面PAD的距离
到平面PAD的距离
求使等式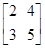 =
=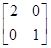 M
M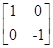 成立的矩阵M.
成立的矩阵M.
对于定义域为A的函数f(x),如果任意的x1,x2∈A,当x1<x2时,都有f(x1)<f(x2),则称函数f(x)是A上的严格增函数;函数f(k)是定义在N*上,函数值也在N*中的严格增函数,并且满足条件f(f(k))=3k.
(1)证明:f(3k)=3f(k);
(2)求f(3k-1)(k∈N*)的值;
(3)是否存在p个连续的自然数,使得它们的函数值依次也是连续的自然数;若存在,找出所有的p值,若不存在,请说明理由.
如图,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(0<y1<y2<…<yn)是曲线C:y2=3x(y≥0)上的n个点,点Ai(ai,0)(i=1,2,3,…,n)在x轴的正半轴上,且△Ai-1AiPi是正三角形(A0是坐标原点).
(1)写出a1,a2,a3;
(2)求出点An(an,0)(n∈N*)的横坐标an关于n的表达式.
已知多项式f(n)= n5+
n5+ n4+
n4+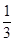 n3-
n3- n.
n.
(1)求f(-1)及f(2)的值;
(2)试探求对一切整数n,f(n)是否一定是整数?并证明你的结论.
已知(1+x)n=a0+a1(x-1)+a2(x-1)2+…+an(x-1)n(n∈N*).
(1)求a0及Sn=a1+a2+a3+…+an;
(2)试比较Sn与(n-2)2n+2n2的大小,并说明理由.