.(选修4—1:几何证明选讲)
如图,已知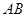 是⊙
是⊙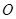 的直径,
的直径,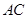 是⊙
是⊙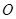 的弦,
的弦,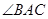 的平分线
的平分线 交⊙
交⊙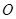 于
于 ,过点
,过点 作
作 交
交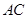 的延长线于点
的延长线于点 ,
, 交
交 于点
于点 .若
.若 ,则
,则 的值为 .
的值为 .
在实数集R中,我们定义的大小关系“>”为全体实数排了一个“序”.类似的,我们在平面向量集 上也可以定义一个称“序”的关系,记为“
上也可以定义一个称“序”的关系,记为“ ”.定义如下:对于任意两个向量
”.定义如下:对于任意两个向量 ,“
,“ ”当且仅当“
”当且仅当“ ”或“
”或“ ”。按上述定义的关系“
”。按上述定义的关系“ ”,给出如下四个命题:
”,给出如下四个命题:
①若 ,则
,则 ;
;
②若 ,则
,则 ;
;
③若 ,则对于任意
,则对于任意 ;
;
④对于任意向量 ,若
,若 ,则
,则 。
。
其中真命题的序号为__________
如图,四边形 是边长为1的正方形,延长
是边长为1的正方形,延长 至
至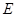 ,使得
,使得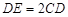 。动点
。动点 从点
从点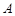 出发,沿正方形的边按逆时针方向运动一周回到
出发,沿正方形的边按逆时针方向运动一周回到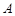 点,
点, .则
.则 的取值范围为________.
的取值范围为________.
在直角坐标系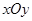 中,已知任意角
中,已知任意角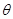 以坐标原点
以坐标原点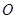 为顶点,以
为顶点,以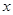 轴的非负半轴为始边,若其终边经过点
轴的非负半轴为始边,若其终边经过点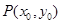 ,且
,且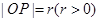 ,定义:
,定义: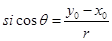 ,称“
,称“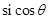 ”为“
”为“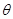 的正余弦函数”,若
的正余弦函数”,若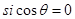 ,则
,则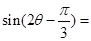 _________.
_________.
某中学为了解学生数学课程的学习情况,在3 000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测,这3 000名学生在该次数学考试中成绩小于60分的学生数是________.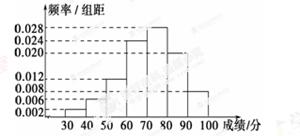
已知函数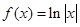 ,则
,则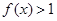 的解集为
的解集为