(本小题满分14分)
已知函数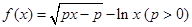 .
.
(Ⅰ)若函数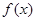 在定义域内为增函数,求实数
在定义域内为增函数,求实数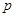 的取值范围;
的取值范围;
(Ⅱ)当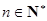 时,试判断
时,试判断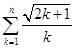 与
与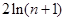 的大小关系,并证明你的结论;
的大小关系,并证明你的结论;
(Ⅲ) 当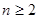 且
且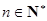 时,证明:
时,证明: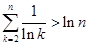 .
.
本小题满分12分)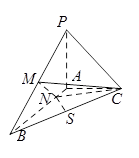
已知三棱锥PABC中,PA⊥平面ABC,AB⊥AC,PA=AC=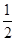 AB,
AB,
N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
(I)证明:CM⊥SN;(II)求SN与平面CMN所成角的大小.
(本小题满分12分)
已知函数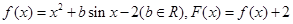 ,且对于任意实数
,且对于任意实数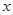 ,恒有
,恒有 .
.
(1)求函数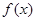 的解析式;
的解析式;
(2)函数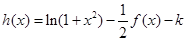 有几个零点?
有几个零点?
(本小题满分12分)
设函数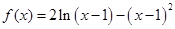 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)若关于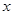 的方程
的方程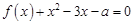 在区间
在区间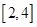 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数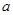 的取值范围.
的取值范围.
(本小题满分12分)
已知向量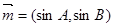 ,
, ,
,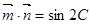 ,且
,且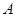 、
、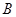 、
、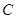 分别为
分别为 的三边
的三边 、
、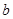 、
、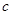 所对的角。
所对的角。
(1)求角C的大小;
(2)若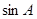 ,
, ,
,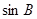 成等差数列,且
成等差数列,且 ,求
,求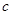 边的长。
边的长。
(本小题满分12分)
已知函数
(1)当x∈[2,4]时.求该函数的值域;
(2)若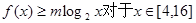 恒成立,求m的取值范围.
恒成立,求m的取值范围.