如图，抛物线y=ax2+bx+2交x轴于A（﹣1，0），B（4，0）两点，交y轴于点C，与过点C且平行于x轴的直线交于另一点D，点P是抛物线上一动点．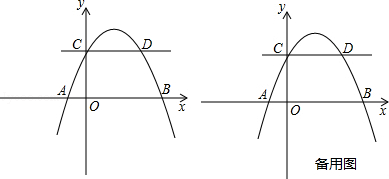
（1）求抛物线解析式及点D坐标；
（2）点E在x轴上，若以A，E，D，P为顶点的四边形是平行四边形，求此时点P的坐标；
（3）过点P作直线CD的垂线，垂足为Q，若将△CPQ沿CP翻折，点Q的对应点为Q′．是否存在点P，使Q′恰好落在x轴上？若存在，求出此时点P的坐标；若不存在，说明理由．
．（本题10分）为了防控冬季呼吸道疾病，某校积极进行校园环境消毒工作，购买了 甲、乙两种消毒液共80瓶，其中甲种每瓶6元，乙种每瓶8元，如果购买这两种消毒液共花去500元，求甲、乙两种消毒液各购买
了多少瓶？
（本题 8 分）两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是40千米/时,水流速度是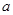
千米/时.2小时后, 乙船比甲船少航行多少千米?
（本题 8 分）一个角的余角与这个角的3倍互补，求这个角的度数．
（本题 8 分，每小题4分）作图：如图，平面内有A，B，C，D四点 按下列语句画图：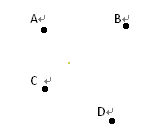
（1）画射线AB，直线BC，线段AC;
（2）连接AD与BC相交于点E.
（本题 8 分）若a、b互为相反数, c是最小的非负数, d是最大的负整数,
求(a+b)d+d－c的值.