超速行驶是引发交通事故的主要原因之一．上周末，小明和三位同学尝试用自己所学的知识检测车速．如图，观测点设在A处，离益阳大道的距离（AC）为30米．这时，一辆小轿车由西向东匀速行驶，测得此车从B处行驶到C处所用的时间为8秒，∠BAC=75°．
（1）求B、C两点的距离；
（2）请判断此车是否超过了益阳大道60千米/小时的限制速度？
（计算时距离精确到1米，参考数据：sin75°≈0.9659，cos75°≈0.2588，tan75°≈3.732，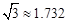
，60千米/小时≈16.7米/秒）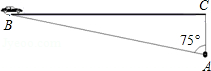
小明和小亮用如下的同一个转盘进行“配紫色”游戏．游戏规则如下：连续转动两次转盘,如果两次转盘转出的颜色相同或配成紫色（若其中一次转盘转出蓝色,另一次转出红色,则可配成紫色）,则小明得1分,否则小亮得1分．你认为这个游戏对双方是否公平？请说明理由．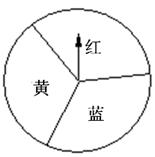
如图,将一付三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
（1）求证：CF∥AB；
（2）求∠DFC的度数.
（1）用配方法解方程：
.
（2）某商品经过连续两次降价,销售单价由原来的125元降到80元,求平均每次降价的百分率．
某新建住宅小区里,有一块三角形绿地如图所示,现准备在其中安装一个照明灯P,使它到绿地各边的距离相等.请你在图中确定安装照明灯P的位置.
已知二次函数图象顶点为C（1,0）,直线
与该二次函数交于A,B两点,其中A点（3,4）,B点在y轴上.
（1）求此二次函数的解析式；
（2）P为线段AB上一动点（不与A,B重合）,过点P作y轴的平行线与二次函数交于点E.设线段PE长为h,点P横坐标为x,求h与x之间的函数关系式；
（3）D为线段AB与二次函数对称轴的交点,在AB上是否存在一点P,使四边形DCEP为平行四边形？若存在,请求出P点坐标；若不存在,请说明理由.