小明和小亮用如下的同一个转盘进行“配紫色”游戏.游戏规则如下:连续转动两次转盘,如果两次转盘转出的颜色相同或配成紫色(若其中一次转盘转出蓝色,另一次转出红色,则可配成紫色),则小明得1分,否则小亮得1分.你认为这个游戏对双方是否公平?请说明理由.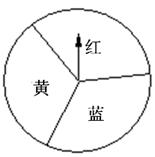
某校数学兴趣小组成员高超对本班上期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析,绘制成如下频数、频率分布表和频数分布直方图.
| 分组 |
49.5~59.5 |
59.5~69.5 |
69.5~79.5 |
79.5~89.5 |
89.5~100.5 |
合计 |
| 频数 |
2 |
a |
20 |
16 |
4 |
n |
| 占调查总人数的 百分比 |
4% |
16% |
m |
32% |
b |
1 |

请你根据图表提供的信息,解答下列问题:
(1)分布表中a= _______ ,b= _______ ;m=,n=。
(2)补全频数分布直方图;
(3)数学老师准备从不低于90分的学生中选1人介绍学习经验,那么取得了97分的高超被选上的百分比是多少?
(4)如图80分以上为优秀,已知该年级共有学生1200人,请你估计一下这次考试优秀人数是多少?
已知:如图,∠A=∠F,∠C=∠D.求证:BD∥CE.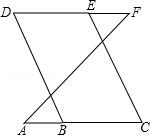
小明家距离学校8千米,今天早晨小明骑车上学途中,自行车突然“爆胎”,恰好路边有便民服务点,几分钟后车修好了,他加快速度骑车到校,我们根据小明的这段经历画了一幅图象,该图描绘了小明行驶路程s与所用时间t之间的函数关系,请根据图象回答下列问题:
(1)小明骑车行驶了多少千米时,自行车“爆胎”修车用了几分钟?
(2)小明共用多长时间到学校的?
(3)小明修车前的速度和修车后的速度分别是多少?
(4)如果自行车未“爆胎”,小明一直按修车前速度行驶,那么他比实际情况早到或晚到多少分钟?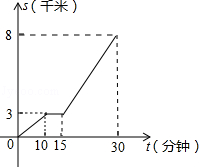
如图,O为直线AB上一点,OC平分∠BOD,OE⊥OC,垂足为O,∠AOE与∠DOE有什么关系,请说明理由.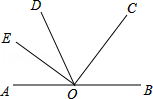
计算下列各题:
(1)(﹣2x3y)2(﹣xy2)(2)(4ab3﹣8a2b2)÷4ab+(2a+b)(2a﹣b)
(3)先化简,再求值:(x+5)(x﹣1)+(x﹣2)2,其中x=﹣2.